저희 A.I. PLUS Lab에서는 자회사인 엑스포넨셜자산운용에서 활용할 인공지능 기반 금융 알고리즘을 연구하고 있습니다. 그 중에서도 저는 페어트레이딩(pairs trading)에 관심을 갖고 있는데요.
페어트레이딩이란 간단히 말해, 유사한 가격 흐름을 갖는 두 상품이 단기적으로 다른 움직임을 보일 때, 가격흐름이 다시 같아질 것을 기대하며 차익거래를 노리는 것을 뜻합니다.

- 출처: https://www.contracts-for-difference.com/cfd-pairs-trading.html
여기서 유사한 가격흐름을 갖는 페어를 찾기 위해 cointegration(공적분)이라는 개념을 이용한다는 것을 알게 되었습니다. 그래서 cointegration 개념에 대해 알아보려 했더니…

- 출처: Peter J.Brockwell, Richard A. Davis, Introduction to Time Series and Forecasting, second edition.
무슨 말인지 도무지 알아들을 수가 없었습니다. 한편, stationary, nonstationary와 같은 단어들이 눈에 띄었습니다. Stationary같은 경우는 이전에 주가 데이터를 학습시키려고 관련 내용을 찾아봤을 때에도 자주 등장하던 단어였거든요. 그런데 그 정의를 엄밀히 살펴본 적이 없기도 했고, 앞서 말한 개념들이 ‘시계열 분석’이라는 과목에서 자세히 다루고 있는 내용이어서 이번 기회에 시계열 분석부터 페어트레이딩까지 이론적 배경에 대해 꼼꼼히 공부하게 되었습니다.
시계열 분석을 공부하다보니 시계열 데이터를 분석하는 큰 흐름 뿐만 아니라, 통계학에서 상식으로 쓰이는 개념들까지도 알 수 있게 되어 꽤 유익했던 것 같습니다. 또한 cointegration이라는 개념이 ‘시계열 분석을 조금만 공부하면 알 수 있겠지…‘라고 생각한 저의 예상과 달리, 과목 후반부에 나오는 고급 개념이었다는 것을 알게 되었고, 덕분에(?) cointegration 개념을 접하는 데까지 매우 긴 여정의 공부를 하게 되었습니다^^; 하지만 다 공부하고 나니 페어트레이딩의 이론적 배경을 무리없이 다 이해할 수 있었어요!
처음에 시계열 분석을 공부하면서 설명이 명쾌하지 않은 부분이 많아서 고생을 했는데, 여러 참고자료와 강의들을 찾아보며 고민하다보니 해결할 수 있었던 것들이 많습니다. 그래서 이번 기회에 정리도 할 겸, 이 내용에 대해 소개하려 합니다. 내용이 굉장히 많기 때문에 곁가지들을 건너뛰고 핵심적인 흐름과 제가 고민했던 부분 위주로 설명을 하려고 하는데, 그럼에도 한 번의 글에 다 담을 수 없어 포스팅을 나눠서 설명하게 될 것 같습니다. 또한 시계열 분석을 소개한 이후에도 여유가 된다면 페어트레이딩에 대해서도, 이론적 배경과 제가 고민한 것들을 소개하려고 합니다.
이번 글에서는 stationarity에 대한 개념과 stationary process의 핵심인 AR(autoregressive), MA(moving average), ARMA(autoregressive moving average) process에 대해 설명합니다. 특히 AR, MA, ARMA를 구분하는데 도움이 되는 ACF(autocorrelation function)와 PACF(partial autocorrelation function)에 대해 알아보고 계산해보는 시간을 가지려합니다. 정확한 정의를 소개해드리기 위해 수식으로 정리할 뿐만 아니라, 직관적으로 받아들이기 쉽게 제 나름대로의 설명을 함께할 예정이니 편하게 보시면 되겠습니다. 실제로 시계열 데이터를 ARMA를 포함한 여러 model로 fitting해보는 과정이라든지, cointegration 등에 관한 내용은 이후 포스팅에 이어서 하겠습니다.
1. Stationarity
우리는 시간의 흐름에 따라 발생하는 데이터를 다룰 때가 많습니다. 매년 GDP, 인구수 등과 같은 통계자료나 주식 가격 등의 데이터가 그렇습니다. 이러한 데이터를 우리는 시계열 데이터(time series data)라고 합니다. 시계열 분석을 한 줄로 요약하자면, 이러한 시계열 데이터가 어떠한 시계열 모델(time series model)에서 발생한 데이터인지 밝히는 과정이라고 할 수 있습니다. 여기서 시계열 모델은 시간에 따른 확률 변수(random variable) $x_t$가 정의되어 있는 확률 과정(stochastic process) ${x_t}{t=1,2,3,\ldots}$(혹은 ${x_t}{t\in\mathbb{Z}}$)으로 표현됩니다. 우리가 관측한 시계열 데이터의 $t$ 번째 값은, 특정 시계열 모델의 $t$ 시점의 확률 변수 $x_t$에서 하나의 값이 실현(realization)된 상태라고 생각하면 됩니다. 일반적으로 시계열(time series)이라는 단어는 시계열 데이터와 시계열 모델을 둘 다 가리킬 수 있기 때문에 상황에 따라 알맞게 받아들여야 합니다.
이제 시계열이라는 개념에 대해 설명했기 때문에 우리는 stationarity를 말할 수 있을 것 같습니다. Stationarity란 간단히 말해, 시계열 모델에서 $x_t$의 확률 분포가 $t$ 에 관계없이 일정한 지를 가리키는 개념이라 생각하면 되는데요. 이러한 성질이 있는 시계열을 stationary time series (model) 또는 stationary (stochastic) process라고 합니다. 크게 strict stationarity와 weak stationarity 두 종류의 정의가 있는데, 수식으로 정리된 각각의 정확한 정의는 아래와 같습니다.
1.1. Definition
1.1.1. Strict stationarity
임의의 확률과정 ${x_t}$에 대해, $F_{x_{t_1},x_{t_2},…,x_{t_k}}(c_1,c_2,…,c_k)$ $=$ $P(x_{t_1}\leq c_1,x_{t_2}\leq c_2,…, x_{t_k}\leq c_k)$를 ${x_t}$의 시점 $t_1,t_2,…,t_k$에 대한 누적 결합 확률 분포라 하면, ${x_t}$가 strict stationary, strong stationary 혹은 strict-sense stationary하다는 것은 아래 조건을 만족한다는 것입니다.
$ F_{x_{t_1},x_{t_2},…,x_{t_k}}(c_1,c_2,…,c_k)=F_{x_{t_1+h},x_{t_2+h},…,x_{t_k+h}}(c_1,c_2,…,c_k) $
$ \forall h, t_1, t_2,…,t_k \in \mathbb{Z} \quad \forall c_1,c_2,…,c_k \in \mathbb{R} \quad \forall k \in \mathbb{N} . $
즉 strict stationary time series에서는 임의의 조합 ${x_{t_1},x_{t_2},…,x_{t_k}}$의 확률적 행동이 (시점이) 평행이동된 조합 ${x_{t_1+h},x_{t_2+h},…,x_{t_k+h}}$의 확률적 행동과 항상 동일하게 됩니다. 특히 위의 정의에서 $k=1$일 때를 살펴보면 시간 $t$ 에 상관없이 매 시점의 개별 확률 분포가 동일해야 함을 알 수 있습니다. 한 마디로 요약하면, strict stationary process는 과거의 확률 분포들 및 그 상호 관계가 미래에도 그대로 유지되는 가장 이상적인 process로 생각할 수 있을것 같습니다.
1.1.2. Weak stationarity
임의의 확률과정 ${x_t}$에 대해, $\mu_t=E[x_t]$, $\gamma(s,t)$ $=$ $Cov(x_s,x_t)$ $=$ $E[(x_s-\mu_s)(x_t-\mu_t)]$라고 하면, ${x_t}$가 weak stationary, stationary in the wide sense, covariance stationary 혹은 stationary in the broad sense하다는 것은 아래 조건을 만족한다는 것입니다.
$\mu_t=\mu_{t+h} \quad \forall t,h \in \mathbb{Z} \quad$ ($\mu_t$는 시간 $t$ 에 의존하지 않음).
$\gamma(s,t)=\gamma(|s-t|,0)=\gamma(t,s) \quad \forall s,t \in \mathbb{Z}$
($\gamma(s,t)$는 $|s-t|$에만 의존. 시계열 분석에서는 시차를 lag라고 하는데, $|s-t|$도 lag에 해당됨).
$V[x_t]=E[(x_t-\mu_t)^2] < \infty \quad \forall t \in \mathbb{Z} \quad$ (${x_t}$는 finite variance process).
여기서 $\gamma(s,t)$는 autocovariance function이라고 하는데, 뒤에서 다시 언급하겠지만 한 process에서 서로 다른 두 시점간의 covariance(공분산)를 표현한 것입니다. Covariance는 직관적으로 두 확률 변수의 선형 의존도를 나타내는 함수라고 생각하면 되는데요. 따라서 독립인 두 확률 변수의 covariance는 0이 됩니다.(역은 성립하지 않습니다. $y=x^2$이고 $x \sim N(0,1^2)$일 때와 같이 서로 의존하는 관계이지만 선형 의존이 아닌 경우에도 covariance는 0이 될 수 있습니다.)
시점의 변화에 상관없이 모든 것(개별 확률 분포, 결합 확률 분포)이 동일해야 했던 strict stationarity보다는 조금 loose하게, 매 시점의 mean(기댓값; 위 정의에서 $\mu_t$)이 변하지 않으면서 두 시점간의 covariance값이 두 시점의 절대치($s,t$)와는 관계없이 둘의 시간차 lag($|s-t|$)에만 의존하면, 이를 weak stationary process라고 함을 알 수 있습니다.
1.1.3. “Weak stationarity is more widely used.”
엄밀하게 모든 확률 분포가 변하지 않는 strict stationary process에 추가로 weak stationary process라는 개념이 정의된 것에 대해 의아한 분들이 있을 수 있습니다. 그리고 실제로(앞으로 이 글에서도) stationary process라 하면 일반적으로 weak stationary process를 가리키는데요. 그 이유는 너무 엄밀한 정의로 인해 어떤 process가 strict stationary인지 이론적으로 밝히는 것은 보통 매우 까다로운 일이고, 주어진 시계열 데이터로부터 수치적으로 strict stationarity를 검증하는 것 또한 매우 ($\times$ 10) 어려운 일이기 때문이라 합니다. 반면 weak stationarity는 mean과 autocovariance function만 살펴보면 되기 때문에 검증이 비교적 용이하고, 이 두 가지 조건만 성립해도 modeling과 forecasting을 하는데에 충분히 안정적이기 때문에 strict stationarity의 조건을 조금 완화시킨 weak stationarity를 주로 사용한다고 합니다. 앞으로 이 글을 포함한 다른 모든 시계열 분석 내용에서 별다른 언급없이 stationarity, stationary process를 말한다면, 그것은 weak stationarity, weak stationary process를 말하는 것이라 생각하시면 됩니다.
1.2. Stationary process
1.2.1. White noise
Stationary process의 가장 대표적인 예는 white noise라고 할 수 있습니다. 이름에서 유추할 수 있듯이, 시계열 데이터에서 불가피하게 섞이는 noise, error등을 표현하기 위해 사용하는데요. 어떤 확률 과정 ${x_t}$가
$E[x_t]=0 \quad \forall t \in \mathbb{Z}$ .
$V[x_t]=\sigma^2 < \infty \quad \forall t \in \mathbb{Z}$ .
$\gamma(s,t)=Cov(x_s,x_t)=0 \quad \forall s \neq t \in \mathbb{Z} \quad$ ($x_s$와 $x_t$가 uncorrelated).
를 만족하면 white noise라고 하고,
$ {x_t} \sim wn(0,\sigma^2) $
와 같이 표기합니다.
실제로는 white noise중에서도 i.i.d.(independent and identically distributed) 조건과 gaussian 조건까지 만족하는 white noise를 사용하는 경우가 많아서 그 정의를 헷갈려할 수 있는데, white noise의 정확한 정의는 위에 언급된 세 가지 조건이 전부입니다. 일반적으로 i.i.d. process는 ${x_t} \sim iid(0,\sigma^2)$와 같이 표기하고, gaussian이 추가되면 ${x_t} \sim iid\ N(0,\sigma^2)$처럼 표기할 수 있습니다. (즉 $iid\ N(0,\sigma^2)$가 실제 모델링을 할 때 많이 쓰이는 white noise라는 말입니다.)
White noise가 정말 stationary process인지는 정의로부터 쉽게 보여지는데요. White noise ${x_t} \sim wn(0,\sigma^2)$에 대해 $\mu_t=E[x_t]$, $\gamma(s,t)=Cov(x_s,x_t)$라 하고, 1.1.2.에서 언급한 stationarity의 세 가지 조건을 만족하는지 체크해보면 아래와 같습니다.
$\mu_t=\mu_{t+h}=0 \quad \forall t,h \in \mathbb{Z}$
$\gamma(s,t)= \begin{cases} \sigma^2, & \forall s,t \in \mathbb{Z} \quad s.t. \ |s-t|=0 \ 0\ , & \forall s,t \in \mathbb{Z} \quad s.t. \ |s-t| \neq 0 \end{cases}$
$V[x_t]=\sigma^2<\infty \quad \forall t \in \mathbb{Z}$
1.2.2. ARMA process
${\varepsilon_t} \sim wn(0,\sigma^2)$일 때, 확률 과정 ${x_t}$가
$ x_t-\phi_1 x_{t-1}-\cdots-\phi_p x_{t-p}=\varepsilon_t+\theta_1 \varepsilon_{t-1}+\cdots+\theta_q \varepsilon_{t-q} \quad \forall t \in \mathbb{Z} \qquad \cdots\cdots \ (1) $
를 만족하면서 동시에 stationary하면 ${x_t}$를 ARMA(p,q) process라고 합니다. (단, 다항식 $(1-\phi_1 z-\cdots-\phi_p z^p)$와 $(1+\theta_1 z+\cdots+\theta_q z^q)$가 공통근을 갖지 않아야합니다.)
만약 $\theta_1=\cdots=\theta_q=0$ 이면 ${x_t}$를 autoregressive process of order p 혹은 AR(p) process라 하고, $\phi_1=\cdots=\phi_p=0$ 이면 moving-average process of order q 혹은 MA(q) process라고 합니다. 쉽게 말해 AR process는 현재값 $x_t$가 이전의 시계열 값들 $x_{t-1}, x_{t-2},…$에 의존하고, MA process는 이전의 noise들 $\varepsilon_{t-1}, \varepsilon_{t-2},…$에 의존하는 확률 과정이라 할 수 있습니다. 그리고 이 두 개의 특징을 함께 갖고 있는 것이 ARMA process입니다.
${x_t}$는 stationary하므로 $E[x_t]$는 $t$ 에 상관없이 상수이고, $(1)$의 양변에 expectation을 취하면 $E[x_t]=0$을 얻게됩니다. 즉 위의 정의는 mean이 0인 ARMA process에 대한 것인데, mean이 $\mu (\neq 0)$인 ARMA(p,q) process는 ${x_t-\mu}$가 위의 조건을 전부 만족하면 되기 때문에, 따로 언급하지 않았습니다.
ARMA process에는 중요한 포인트가 몇 가지 있습니다. 첫번째로는 ARMA process가 $(1)$의 조건을 만족하면서 stationary 해야한다는 점, 두번째로는 위에서 white noise $\varepsilon_t$와 $x_t$의 관계에 대해 특별한 제약을 하지 않았는데, 현실에서는 $\varepsilon_t$는 과거의 $x_s(s<t)$와 uncorrelated라고 가정한다는 점입니다. 이 부분을 설명하기 위해, backshift operator와 causal process에 대해 잠깐 짚고 넘어가도록 하겠습니다.
Backshift operator
임의의 확률 과정 ${x_t}$에 대해 $B^jx_t=x_{t-j}$의 변환을 하게하는 operator $B$를 backshift operator라고 합니다. ( $j<0$일 땐 forward-shift operator라고 하기도 합니다.) Backshift operator를 사용하면 위 $(1)$의 조건식은 아래와 같이 표현이 가능합니다.
$ (1-\phi_1 B-\cdots-\phi_p B^p)x_t=(1+\theta_1 B+\cdots+\theta_q B^q)\varepsilon_t $
여기서 두 다항식 $\phi(z)=1-\phi_1 z-\cdots-\phi_p z^p$, $\theta(z)=1+\theta_1 z+\cdots+\theta_q z^q$을 정의하면, 위 식에서 $x_t$와 $\varepsilon_t$의 계수를 $B$에 대한 다항식과 같이 생각할 수 있고, 따라서 $(1)$은
$ \phi(B)x_t=\theta(B)\varepsilon_t \qquad \cdots\cdots \ (2) $
와 같이 더 간단한 형태로 적을 수 있게됩니다. 특히 여기서 $\phi(z)$는 characteristic polynomial이라고 하기도 합니다. (또한, $\phi(B)$와 $\theta(B)$는 각각 autoregressive operator, moving-average operator라고 부릅니다.)
이렇게 $(2)$와 같이 operator에 대한 다항식으로 적는 이유는 실제로 이것들이 다항식과 동일한 연산이 가능하기 때문인데요. 실제로 $\phi(B)$, $\theta(B)$에 대해 인수분해나 약분, $B$에 대한 다항식을 양변에 곱하는 등의 연산을 시행해도 $(2)$식에는 문제가 없습니다. 따라서 위의 ARMA process 정의에서, ‘단, 다항식 $(1-\phi_1 z-\cdots-\phi_p z^p)$와 $(1+\theta_1 z+\cdots+\theta_q z^q)$가 공통근을 갖지 않아야합니다.’라고 한 이유는, 만약 두 다항식에 공통근이 존재하면 $\phi(B)$, $\theta(B)$이 약분이 되어 차수가 낮아지게 되고, 그러면 더이상 ARMA(p,q) process라고 할 수 없기 때문입니다. (p,q보다 더 작은 order를 갖는 ARMA process로 다시 불려야 할 것 입니다.)
Stationarity of ARMA and causal process
ARMA의 정의에서 짐작할 수 있듯이, $(1)$식을 만족하는 것만으로는 ${x_t}$의 stationarity가 보장되지 않습니다. 예를 들어 ${x_t}$가
$ x_t - \phi_1 x_{t-1} = \varepsilon_t $
와 같은 조건식을 만족하더라도, $\phi_1=1$인 경우는 $x_t$가 non-stationary하게 되는데요. (이는 뒤에 언급될 random walk라는 non-stationary process의 일종입니다.) 위의 경우와 비슷하게, 일반적으로
$ \phi(B)x_t=\theta(B)\varepsilon_t \qquad \cdots\cdots \ (2) $
에서는 $\phi(z)$가 $|z|=1$(unit circle)에서 근을 갖지 않으면 ${x_t}$가 stationary하고, ARMA process가 되게 됩니다.
이유를 간단히 설명하면 $\phi(z)$가 $|z|=1$(unit circle)에서 근을 갖지 않는 경우, $\phi(z)^{-1}=\sum_{j=-\infty}^\infty\ \chi_jz^j = \chi(z)$ ($\chi_j$는 absolutely summable)와 같이 표현할 수 있어서 식 $(2)$는
$ x_t=\phi(B)^{-1}\theta(B)\varepsilon_t=\underset{j=-\infty}{\overset{\infty}{\sum}}\ \psi_j\varepsilon_{t-j} \qquad \cdots\cdots \ (3) $
와 같이 변형할 수 있는데($\psi_j$는 absolutely summable), 이러한 경우 $x_t$가 stationary함을 쉽게 알 수 있습니다. (자세한 설명은 참고자료를 찾아보시면 됩니다.)
그런데 $(3)$의 식을 살펴보면, $x_t$의 표현식에 미래의 noise $\varepsilon_s (s>t)$가 들어가 있는 것을 알 수 있습니다. 이러한 상황은 현실에서는 자연스러운 상황이 아닌데요. 그래서 ARMA process ${x_t}$에 대해, $x_t$가 $\varepsilon_s(s \leq t)$들만 이용해서 표현 가능한 경우를 ($x_t=\sum_{j=0}^\infty \psi_j\varepsilon_{t-j}$의 꼴) causal하다고 정의하여 따로 분류하고 있습니다. 즉 causal process는 미래에 발생하는 noise $\varepsilon_t$가 과거의 시계열 값 $x_i\ (i<t)$과 uncorrelated된 채로 발생합니다. (혹은 과거의 시계열 값이 미래의 noise와 uncorrelated합니다.) 사실 정확한 정의는 좀 더 복잡하지만, 이것에 대해 길게 논의할 필요가 없다 생각되어 간단히만 정의하였습니다.
결론부터 얘기하면, causal한 ARMA process가 되기위한 필요충분조건은 $\phi(z)$의 근이 $|z| > 1$ 에만 존재하는 것인데요. $\phi(z)$의 근이 $|z| > 1$ 에만 존재하는 경우, $\phi(z)^{-1}=\sum_{j=0}^\infty\ \chi_jz^j = \chi(z)$와 같이 표현할 수 있고($j$가 0부터 시작함에 유의하세요), 식 $(2)$가
$ x_t=\phi(B)^{-1}\theta(B)\varepsilon_t=\underset{j=0}{\overset{\infty}{\sum}}\ \psi_j\varepsilon_{t-j} \qquad \cdots\cdots \ (3) $
와 같이 표현할 수 있게 되어 causal process가 되게됩니다.
다시 말해 ARMA process ${x_t}$의 이론적 정의는 ${x_t}$가 $(1)$의 조건식을 만족하며 $\phi(z)$가 $|z|=1$(unit circle)위에서 근을 갖지 않는 것인데, 이 중에서도 $\phi(z)$가 $|z|>1$에서만 근을 갖는 경우는 causal하다고 하여 따로 구분해 놓았고, uncausal한 ARMA process는 $x_t$의 표현식에 미래의 noise term이 섞이게 되어 현실에서는 사용하기 힘든 부자연스러운 모델이라는 것입니다. 그리고 실제로도 uncausal한 모델은 거의 사용되지 않기 때문에, ARMA process라 하면 일반적으로 causal한 ARMA process만을 일컫게 됩니다.
이러한 구분 방식이 오히려 복잡하게 들릴 수도 있지만, AR(1) process를 예시로 생각해보면 지금까지 설명한 것들로 인해 앞으로 우리가 다루게 될 ARMA process가 간단히 어떤 특징인지 알 수 있을 것 입니다.
$ x_t = \phi_1 x_{t-1}+\varepsilon_t \quad (|\phi_1| \neq 1) $
위와 같은 관계식을 생각하면, characteristic polynomial이 $\phi(z)=1-\phi_1 z$가 되기 때문에 근의 크기가 1보다 크기위한 조건은 $|\phi_1|<1$임을 알 수 있습니다. 실제로 엑셀같은 프로그램을 이용하여, $x_0=0$으로 두고 white noise series를 $t=0$부터 독립적으로 생성하며 $|\phi_1|<1$인 경우에 대해 위의 process가 실현된 값을 plotting을 해보면 mean근처에서 굉장히 안정적으로 진동하는 것을 확인할 수 있는데요. $|\phi_1|>1$의 경우를 같은 방법으로 plotting을 하면 매우 빠르게 발산하게 되는 것 또한 쉽게 알 수 있습니다. 이 경우에는 white noise가 이전의 시계열 값들에 의존하여 생성된다는 사실이 적용되지 않은채로 독립적으로 생성하여 plotting했기 때문인데요. 만약 이를 해결하기 위해 안정적인 plotting을 보이는 방향으로 white noise를 생성하려고 시도한다면, 그것은 매우 어렵고 부자연스러운 행동임을 알게 될 것입니다. 즉 AR(1) process라 하면 이론상으로는 위의 조건식을 만족하면서 stationary한 process 전부를 가리키지만$(|\phi_1| \neq 1)$, 우리는 $|\phi_1|<1$인, causal하면서 stationary한 경우만 현실에서 다루게 되고, 일반적인 ARMA process에서도 이는 동일하게 적용된다는 것을 알고 있으셔야 합니다.
1.3. Non-stationary process
Non-stationary process의 예로는 random walk가 있습니다. Random walk는 선형 트렌드에 white noise가 누적으로 더해져 있는 time series model로서,
$ x_t = \delta + x_{t-1} + \varepsilon_t \ , \quad {\varepsilon_t} \sim wn(0,\sigma^2) $
혹은
$ x_t = \delta t + \underset{i=0}{\overset{t}{\sum}}\ \varepsilon_i \ , \quad {\varepsilon_t} \sim wn(0,\sigma^2) $
와 같은 식을 만족하는 확률 과정 ${x_t}$를 말합니다. $(\delta$ 는 상수.$)$
Random walk는 정의를 살펴보았을 때 (두번째 식에서 양변에 variance를 취하면) $V[x_t]=(t+1)\sigma^2$임을 알 수 있는데요. $V[x_t]$는 lag가 0인 covariance로서, stationary process의 경우에는 이 값이 $t$에 상관없이 일정해야 합니다(일반적으로 $V[x_t]=\gamma(t,t)$이고, stationary의 경우에는 $V[x_t]=\gamma(0,0)$으로 일정해야함). 그런데 random walk의 경우에는 시간이 지남에 따라 $V[x_t]$가 증가하기 때문에, stationary process가 될 수 없는것 입니다. 대표적으로 주가의 로그값이 random walk process를 따른다고 알려져있고, 이외에도 여러 경제 지표들을 모델링하는데도 쓰이고 있습니다.
1.4. Property of stationarity
시계열 분석에서 stationarity 개념을 도입하여 이를 중요하게 다루는 이유에 대해 궁금하신 분들이 있을 수 있습니다. 이것은 사실 굉장히 중요한 부분이라 생각되는데, 그 이유는 stationary process는 mean-reverting(평균 회귀)의 성질이 있다고 여길 수 있기 때문입니다. 어떠한 시계열 데이터가 있고 이 데이터에 fit하는 model이 stationary일 가능성이 높아 보인다면, 이 시계열은 미래에도 평균적으로 model의 constant mean의 값을 $(E[x_t])$ 보일 것으로 예측할 수 있습니다. 특히 가장 마지막 시계열 값이 model의 mean과 차이를 많이 보이고 있는 경우, 가까운 미래에는 이 시계열이 mean값의 방향으로 변화할 것이라 추측할 수 있고 이것이 앞서 말한 mean-reverting 성질이 되는 것 입니다.
$x_t=\phi x_{t-1}+\varepsilon_t \ (\varepsilon_t \sim wn(0,\sigma_1^2),\ |\phi|<1)$인 AR(1) model과 $y_t=y_{t-1}+\xi_t \ (\xi_t \sim wn(0, \sigma_2^2))$인 random walk (trend term $\delta$가 없는 simple random walk)를 비교해보면 stationarity의 성질이 어떤 차이를 만들어내는지 더 이해하기 쉽습니다. ${x_t}$와 ${y_t}$가 가장 최근에 생성한 시계열 값이 모두 10이라고(적당히 0에서 먼 값) 가정해봅시다. ${x_t}$는 mean과 variance가 각각 0, $\frac{\sigma_1^2}{1-\phi^2}$으로 상수인 stationary process이기 때문에, 이후의 시계열 값들에 대해 0의 방향으로 변화할 것이라는 추측을 할 수 있습니다(10이라는 값에서 mean으로부터 더 멀어질 확률은 적을 것이라 생각할 것 입니다). 하지만 ${y_t}$는 non-stationary process입니다. 이 경우에는 simple random walk라 mean은 0으로 상수이지만, 그래도 variance가 계속 커지는 process이기 때문에, 다시 0으로 돌아올 것이라는 추측을 함부로 할 수 없습니다. $y_t=y_{t-1}+\xi_t$의 관계식을 살펴보면 이전값과 다음값의 차이가 평균이 0인 noise가 추가되는 것이 전부이기 때문에, 우리는 가장 마지막에 10이라는 시계열 값을 얻어도 그 이후에도 ‘평균적으로 10의 값이 나오겠구나’ 하고 예측할 수 밖에 없는 것입니다.
Mean-reverting뿐만 아니라 stationary process가 갖고 있는 여러 특징들로 인해, stationarity는 시계열 분석에서 중요한 역할을 하고있습니다. 앞에서 알아본 것과 같이 미래의 시계열 값을 예측(forecasting)을 할 때에도 그렇고, 시계열 데이터에 fit하는 시계열 모델을 찾을 때에도 stationarity의 개념은 빠질수 없습니다. 또한 시계열 분석 학문외에서도, mean-reverting 성질이 introduction에서 언급한 페어트레이딩(pairs trading) 가설의 바탕이 되는 등 그 개념이 중요하게 여겨지고 있습니다.
2. ACF, PACF
ACF와 PACF는 각각 autocorrelation function과 partial autocorrelation function을 가리키는 단어로서, 하나의 time series model에서 서로 다른 두 시점의 확률 변수에 대한 상관관계를 나타내는 개념입니다. 즉 input이 두 시점이 되고, 예를 들어 ACF는 $\rho(s,t)$와 같이 표기하게 됩니다. Stationary process의 경우에는 정의에 의해 ACF, PACF 모두 두 시점의 차이인 lag에만 의존하게 되는데요. 따라서 stationary process에 한해서는 ACF, PACF의 input을 lag 하나로 표시하게 되어 ACF의 경우에는 $\rho(h)$와 같이 나타내게 됩니다 ($\rho(s,t)=\rho(|s-t|,0)=\rho(h,0)$의 마지막 항에서 0을 생략한 것입니다). 특히 이 때 lag에 따른 ACF, PACF의 그래프는 AR, MA, ARMA model을 구분 짓는 중요한 기준이 되므로 잘 알아둘 필요가 있습니다.
2.1. Definition
2.1.1. ACF
ACF에 대해 설명하기 전에, 먼저 autocovariance function(일부 자료에서는 ACVF로 줄여 쓰기도 합니다)을 알아야 하는데요. 확률 과정 ${x_t}$가 있을 때, autocovariance function $\gamma_x(t_1,t_2)$는
$ \gamma_x(t_1,t_2) = Cov(x_{t_1},x_{t_2}) = E[(x_{t_1}-E[x_{t_1}])(x_{t_2}-E[x_{t_2}])] $
와 같이 정의됩니다.
앞에서 stationarity를 정의할 때도 간단히 언급했지만, 결국에 autocovariance는 covariance 개념이기 때문에 직관적으로 한 process에서 두 시점의 선형 관계 세기(의존도)를 표현한 것이라 생각하면 될 것 같습니다. 특히 ${x_t}$가 stationary process라면 autocovariance는 두 시점의 차이(lag)에만 의존하기 때문에 $\gamma(s,t)=\gamma(|s-t|,0):=\gamma(|s-t|)$와 같이 autocovariance를 일변수 함수로 표현할 수 있고, lag $|s-t|$를 $h$로 표기하면,
$ \gamma_x(h) = Cov(x_{t+h},x_t) = E[(x_{t+h}-\mu)(x_t-\mu)] $
와 같이 쓸 수 있습니다. $(\mu = E[x_t] = E[x_{t+h}])$
이제 ACF에 대해 정의할 수 있는데요. 두 확률 변수의 correlation과 covariance가 어떤 차이인지 알고 있다면, ACF 또한 autocovariance function과 어떤 관계인지 쉽게 유추할 수 있습니다. ACF(autocorrelation function) 는 autocovariance function을 두 시점의 확률 변수의 표준편차로 나눠서 얻게 됩니다.
$ \rho_x(t_1,t_2) = \frac{\gamma_x(t_1,t_2)}{\sigma_{x_{t_1}}\sigma_{x_{t_2}}} = \frac{Cov(x_{t_1},x_{t_2})}{\sigma_{x_{t_1}}\sigma_{x_{t_2}}} $
Stationary model에서는 autocovariance와 마찬가지로 ACF를 lag h에 대한 함수로 표현할 수 있고, 조금 더 간단히 정리될 수 있습니다.
$ \rho_x(h) = \frac{\gamma_x(h)}{\sigma_{x_{t+h}}\sigma_{x_t}} = \frac{Cov(x_{t+h},x_t)}{\sigma_{x_t}^2} = \frac{Cov(x_{t+h},x_t)}{Cov(x_t,x_t)} (= \frac{\gamma_x(h)}{\gamma_x(0)}) $
Correlation이 covariance로부터 계산되어 두 확률변수간의 선형 의존도를 -1과 1사이의 값으로 표현한 것이듯이, ACF 또한 한 process의 서로 다른 두 시점의 선형 의존도를 -1과 1사이의 값으로 표현한 것이라 생각할 수 있습니다. ACF는 stationary process에서 lag에 따라 그래프를 그려 사용하는데요. White noise의 경우에는 lag가 0일 때를 제외하고는 ACF의 값이 전부 0이 됨을 쉽게 알 수 있습니다. (lag 0일 때 ACF는 항상 1). 아래는 어떤 시계열 데이터에 대해 sample ACF를 계산해 ACF를 추정한 것인데요. 점선 사이의 값은 거의 0이라 간주했을 때, white noise의 ACF 그래프와 거의 비슷하므로 데이터가 발생한 모델이 white noise이라고 추정할 수 있습니다.
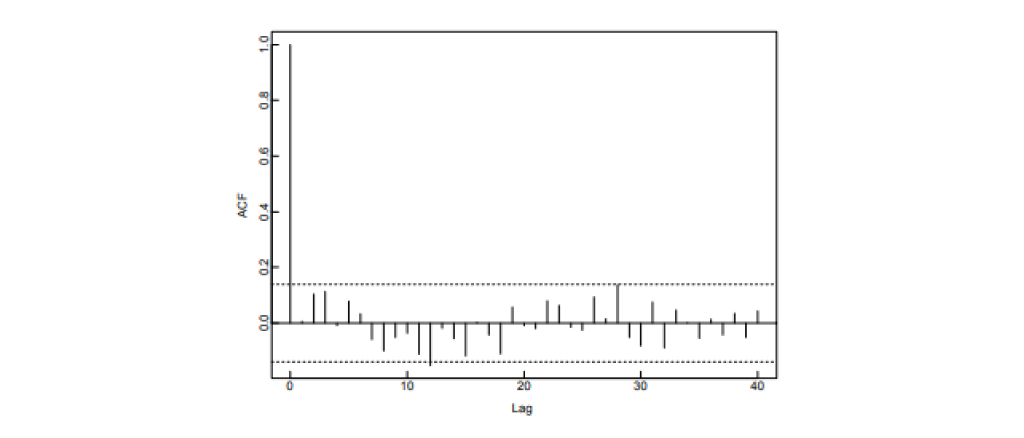
- 출처: Peter J.Brockwell, Richard A. Davis, Introduction to Time Series and Forecasting, second edition.
2.1.2. PACF
PACF의 정의를 알기 위해서는 partial correlation에 대해 알 필요가 있습니다. 먼저, 확률 변수 $X$,$Y$ 그리고 $\mathbf{Z}=(Z_1,\ldots,Z_n)$이 있다고 할 때, $Z_1,\ldots,Z_n$에 대한 $X$,$Y$의 partial correlation은 $\rho_{XY \cdot \mathbf{Z}}$로 표기하는데요. $X$,$Y$를 $Z_1,\ldots,Z_n$으로 선형 회귀 시켰을 때 남는 잔차를 각각 $e_X$,$e_Y$라고 하면 이 둘의 correlation을$(\rho(e_X,e_Y))$ 계산함으로써 $\rho_{XY \cdot \mathbf{Z}}$가 얻어집니다.
왜 이런 개념을 도입하였는지 설명하기 위해, 매년 교회의 수$(X)$와 범죄자의 수$(Y)$의 데이터에 대해 상관관계(correlation)을 구하려고 하는 상황을 상상해봅시다. 둘은 모두 매년 인구수$(\mathbf{Z}=Z_1)$와 양의 상관관계를 갖기 때문에, 단순히 둘$(X, Y)$의 상관관계$(\rho(X,Y))$를 구하면 양의 상관관계가 존재하는 것으로 나타날 수 있습니다. Partial correlation은 이러한 상황에서 인구수의 영향을 제거하고 오로지 둘만의 상관관계를 구하기위해 도입된 개념이라 생각하면 되는데요. 정의를 적용해보면, 교회의 수와 범죄자의 수를 인구수로 선형 회귀 시킨 후, 그 때 생기는 잔차들 간의 상관관계를 구함으로써 partial correlation을 계산할 수 있습니다.
Time series model에서는 두 시점의 partial correlation을 구할 때, 두 시점의 사이에 있는 시점들을 세 번째 확률변수 $\mathbf{Z}$로 여겨, 그 영향을 제외하고 상관관계를 구하고, 이를 PACF(partial autocorrelation function) 이라 합니다. 확률 과정 ${x_t}$에 대해,
$ \alpha_x(t_1,t_2)=\rho_{x_{t_1}x_{t_2}\cdot X} \quad (X=(x_{t_1+1},\ldots,x_{t_2-1})) $
와 같이 PACF가 정의되고, 정의에 의해 $|t_1-t_2|\leq 1$ 일 때는 ACF와 동일한 식이 됨을 알 수 있습니다.
ACF와 마찬가지로, stationary process의 경우에 PACF는 lag에만 의존하게 되고, lag를 input으로 받는 함수로 표기하게 됩니다.
$ \alpha_x(h)=\rho_{x_{t+h}x_t\cdot X} \quad (X=(x_{t+1},\ldots,x_{t+h-1})) $
추가적으로 여기서 증명할 수는 없지만, ARMA process ${x_t}$에 한하여 PACF를 계산하는 다른 방법도 존재합니다. 이를 굳이 언급하는 이유는 실제 데이터에서 PACF를 추정할 때(sample PACF를 계산할 때), PACF의 정의가 아닌 아래 관계식을 바탕으로 추정하기 때문인데요. $\gamma_x(h)$를 ${x_t}$의 lag $h$에 대한 autocovariance라 할 때,
$ \Gamma_h \bar{\phi}_h = \bar{\gamma}_h $
$ \bar{\gamma}_h = \begin{pmatrix} \gamma_x(1) \ \gamma_x(2) \ \vdots \ \gamma_x(h) \end{pmatrix} $
와 같이 정의된 ($\phi_{h1}, \ldots, \phi_{hh}$에 대한) 방정식을 풀어 해를 구하면, 그 중 $\phi_{hh}$가 PACF $\alpha_x(h)$와 같게됨이 알려져 있습니다.
$ \alpha_x(h) = \phi_{hh} \quad if \; {x_t} \; is \; ARMA \; process . $
2.2. Examples
ACF, PACF를 소개하는 도입부에서 이들의 그래프 모양은 AR, MA, ARMA process를 구분 짓는 기준이 된다고 언급했습니다. 임의의 ARMA process에 대해 ACF, PACF를 계산하여, 모든 상황에 따라 그래프 모양이 어떻게 달라지는지 한 번에 보고 싶지만, 계산이 꽤 복잡한 관계로 몇 가지만 예시로 계산해보려고 합니다. 일반적인 상황도 예시와 크게 다르지 않기 때문에, 간단한 process들에 대해 ACF와 PACF를 계산해본 후 전체적인 경향을 정리하도록 하겠습니다.
2.2.1. ACF of MA(1)
먼저,
$ x_t = \varepsilon_t + \theta \varepsilon_{t-1} , \quad {\varepsilon_t} \sim wn(0, \sigma^2) $
를 만족하는 MA(1) process ${x_t}$에 대해 ACF를 계산해 보겠습니다.
$ \gamma_x(h) = Cov(x_{t+h},x_t) = Cov(\varepsilon_{t+h} + \theta \varepsilon_{t+h-1}, \varepsilon_t + \theta \varepsilon_{t-1}) $
$ = Cov(\varepsilon_{t+h} , \varepsilon_t) + \theta Cov(\varepsilon_{t+h} , \varepsilon_{t-1}) + \theta Cov(\varepsilon_{t+h-1} , \varepsilon_t) + \theta^2 Cov(\varepsilon_{t+h-1} , \varepsilon_{t-1}) $
$ =\begin{cases} (1+\theta^2)\sigma^2 , & if \; h=0 \ \theta \sigma^2 , & if \; h=1 \ 0\ , & if \; h > 1 \end{cases} $
와 같이 autocovariance가 계산되므로 ACF는 아래와 같게 됩니다. (ACF, PACF는 우함수이므로 $h \geq 0$에 대해서만 나타내면 됩니다.)
$ \rho_x(h)= \begin{cases} 1\ , & if \; h=0 \ \frac{\theta}{1+\theta^2}\ , & if \; h=1 \ 0\ , & if \; h > 1 \end{cases} $
일반적으로 MA(q) process에 대해서도 동일한 계산과정을 진행하면, $h>q$일 때는 ACF가 항상 0이 됨을 알 수 있습니다.
2.2.2. ACF of AR(2)
다음으로는
$ x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \varepsilon_t , \quad {\varepsilon_t} \sim wn(0, \sigma^2) \quad \cdots \cdots \ (4) $
을 만족하는 AR(2) process ${x_t}$에 대해 ACF를 계산해 보겠습니다.
$E[x_t]=0$이므로 $\gamma_x(h)=\gamma_x(-h)=Cov(x_{t-h},x_t)=E[x_{t-h}x_t]$가 되고, 따라서 위 $(4)$식의 양 변에 $x_{t-h}$를 곱한 후 expectation을 취하게 되면 아래와 같은 식을 얻게됩니다.$(h>0)$
$ \gamma_x(h) = \phi_1 \gamma_x(h-1) + \phi_2 \gamma_x(h-2) + E[x_{t-h}\varepsilon_t] $
$ = \phi_1 \gamma_x(h-1) + \phi_2 \gamma_x(h-2) + Cov(x_{t-h}, \varepsilon_t) = \phi_1 \gamma_x(h-1) + \phi_2 \gamma_x(h-2) $
(${x_t}$는 앞서 언급하였듯이 causal한 process로 간주합니다.)
위에서 $\gamma_x(h)$에 대한 점화식을 얻었는데, 특성방정식 $y^2-\phi_1 y-\phi_2=0$의 두 근을 $y_1,y_2$라 하면, 이 때 $\gamma_x(h)$가
$ \gamma_x(h) = c_1y_1^h + c_2y_2^h $
와 같이 해를 갖는 것이 알려져 있습니다. $\rho_x(h)=\gamma_x(h)/\gamma_x(0)$이므로 이로써 ACF를 구할 수 있게 되었습니다.
특히 여기서 특성방정식의 근 $y_i$들이 크기가 1보다 작은 복소수 범위의 값이기 때문에(causal하기 위한 조건으로 부터 $\phi(z)$의 근이 unit circle의 외부에 있어야하고, 이것의 역수가 특성방정식의 근이 되기 때문에 $y_1,y_2$가 unit circle의 내부로 들어가게 됨을 알 수 있습니다.), ACF는 exponential하게 감소하는 그래프 혹은 양과 음을 넘나들며 감쇠진동하는 그래프(damped sine wave) 둘 중에 하나의 모양이 됨을 알 수 있습니다. 실제로 임의의 AR(p) process에 대해서도 ACF를 계산해보면 이러한 모양의 그래프가 나타나게 됩니다.
2.2.3. PACF of AR(1)
PACF도 하나의 예시에 대해 계산해보고 넘어가겠습니다. 결론부터 말하면, PACF는 AR, MA process에 대해 ACF와 정확히 반대의 모습을 보이는데요. 즉, AR(p) process에 대해서는 PACF가 p보다 큰 lag에 대해 항상 0의 값이 나오게 됩니다. 반대로, MA(q) process에 대해서는 PACF가 exponential하게 감소하거나 감쇠진동하는 사인파 모양을 띠는데요. 여기서는 AR(1) process에 대해서만 간단히 계산해보도록 하겠습니다.
$ x_t = \phi x_{t-1} + \varepsilon_t , \quad {\varepsilon_t} \sim wn(0, \sigma^2) \quad \cdots \cdots \ (5) $
를 만족하는 AR(1) process ${x_t}$에 대해, $\alpha_x(h)=\alpha_x(-h)=\rho_{x_t,x_{t-h} \cdot (x_{t-1},…,x_{t-h+1})}$를 계산을 해야하는데, 그러려면 먼저 $x_t$와 $x_{t-h}$를 $(x_{t-1},…,x_{t-h+1})$로 선형 회귀 시키고 잔차를 구해야합니다. (여기서 $h \leq 1$인 경우는 ACF와 동일하기 때문에, $h>1$인 경우에 대해서만 생각하면 됩니다.)
그런데 $(5)$의 관계식에서 우리는 $x_t$를 $(x_{t-1},…,x_{t-h+1})$로 선형 회귀를 시키면 계수가 $(\phi, 0, 0, …, 0)$이고 잔차가 $\varepsilon_t$가 됨을 알 수 있습니다. 따라서 $x_{t-h}$를 $(x_{t-1},…,x_{t-h+1})$로 선형 회귀 시키고 남은 잔차를 (계수는 모르지만) $x_{t-h}-c_1 x_{t-1}-…-c_{h-1}x_{t-h+1}$라 한다면,
$ \alpha_x(h)=\rho(\varepsilon_t, x_{t-h}-c_1 x_{t-1}-…-c_{h-1}x_{t-h+1}) $
가 됨을 알 수 있고, $x_{t-1},…,x_{t-h+1}$는 모두 $\varepsilon_t$와 uncorrelated 되어 있기 때문에 $\alpha_x(h)$가 0이 됨을 알 수 있습니다. 즉 AR(1) process에 대해서는 $h>1$인 경우 PACF가 항상 0이 나오게 됩니다.
2.3. Classification of ARMA
지금까지 간단한 process들에 대해 ACF와 PACF를 계산해봤는데요. 가장 일반적인 ARMA process를 포함하여 계산해보지 않은 경우들이 남아있지만 앞서 계산한 예시들을 통해 어떤 흐름인지 파악하셨을거라 생각합니다. ARMA process의 경우에는 ACF, PACF 모두 exponential하게 감소하거나 감쇠진동하는 사인파 그래프 모양만을 보이는데요. 전체적인 경향을 표로 정리하면 아래와 같습니다.
| Process | ACF | PACF |
|---|---|---|
| AR(p) | Exponential하게 감소하거나 damped sine wave (tails off) |
lag p 이후에 0 (cut off after lag p) |
| MA(q) | lag q 이후에 0 (cut off after lag q) | Exponential하게 감소하거나 damped sine wave (tails off) |
| ARMA(p,q) | Exponential하게 감소하거나 damped sine wave (tails off) |
Exponential하게 감소하거나 damped sine wave (tails off) |
(여기서 tails off는 그래프가 1에서 0으로 점차 감소함을, cut off는 어느 순간 그래프가 0의 값만을 갖는 상황을 말하는 것입니다.)
실제로는 process를 먼저 알고있는 상황이 아니기 때문에, 가지고 있는 시계열 데이터로 부터 sample ACF와 sample PACF를 계산하고, 이로부터 데이터가 어떤 process에서 나오게 된 것일지 추측하게 되는데요. 이 때 위의 결과를 이용하여 AR인지, MA인지, ARMA인지, AR이라면 AR(p)에서 p가 몇인지 등에 대한 정보를 추정된 ACF, PACF 그래프에서 얻게됩니다. (만약 sample ACF가 lag 3 이후에 cut off 되고 sample PACF가 exponential하게 감소하는 모양을 띤다면, 갖고있는 시게열 데이터는 MA(3) model로부터 발생한 것이라 추측할 수 있게되는것 입니다.)
3. Conclusion
지금까지 시계열 분석의 가장 핵심이라 할 수 있는 stationarity 개념과 ARMA, ACF, PACF 등에 대해 살펴보았는데요. 지금까지의 내용은 이론적인 내용일 뿐, 실제로는 우리에게 어떤 시계열 데이터가 주어졌을 때 이것이 stationary process(에서 발생한 것)인지, 그렇다면 이 process의 ACF와 PACF는 어떻게 되는지, 이런 것들에 대해 추정하는 방법은 담겨있지 않습니다. 하지만 기초 개념들의 정의와 직관, 여러 결과들을 얻기위한 계산 방식 등을 알아야만 실제 시계열 데이터를 분석하고 모델을 추정하는 원리를 알 수 있기 때문에 이 부분은 절대 빠질 수 없는 부분이라고 생각합니다.
앞으로 남은 포스팅에서는, 우리에게 시계열 데이터가 주어졌을 때 기본 통계량 추정을 하는 법과 이를 통해 stationary, nonstationary process로 모델링을 하는 다양한 종류의 방법에 대해 소개할 예정입니다. 이것들에 대해 잘 전달이 된다면 cointegration 관계란 무엇인지에 대해서도 짚고 넘어갈 수 있을 것 같습니다. 읽어주셔서 감사합니다.
참고문헌
시계열 분석 강의 - 이기천 교수
Robert H.Shumway, David S. Stoffer, Time Series Analysis and Its Applications, fourth edition.
Peter J.Brockwell, Richard A. Davis, Introduction to Time Series and Forecasting, second edition.