지난 ‘ 시계열 분석과 페어트레이딩 part.1 ‘에서는 stationarity의 개념과 ARMA process 및 ACF, PACF에 대해 자세히 살펴보았습니다. 시계열 모델은 크게 stationary process와 non-stationary process로 나뉘고, stationary process의 핵심에 ARMA process가 있다는 것을 알게되었는데요. 마지막에는 일부 ARMA process의 ACF와 PACF를 계산하며, 특징을 정리하는 시간을 가졌습니다.
그런데 시계열 모델에 대해서만 아는 것으론 충분하지 않습니다. 시계열 분석은 시계열 데이터에 대해 적합한 시계열 모델을 찾는 과정이기 때문에, 어떤 시계열 모델을 사용할지 정하는 과정 또한 알아둘 필요가 있습니다. 모델링(modeling)이라 부르는 이 과정은 시계열 데이터로부터 ACF 등의 통계량(statistics)을 추정(estimation)하는 것에서 시작합니다.
시계열 데이터로부터 추정된 mean, ACF, PACF는 sample이라는 단어를 붙여 sample mean, sample ACF, sample PACF라고 하고, 실제 mean, ACF, PACF의 정의를 바탕으로 추정하게 되는데요. 이렇게 통계량 추정을 한 후, 시계열 데이터가 stationary process로 (모델링이 가능해) 보이는 경우엔 적합한 ARMA model을 찾는 과정을 거치고, 그렇지 않은 경우엔 데이터를 변환하거나 non-stationary model을 이용하는 등의 다른 시도를 하게 됩니다.
이번 글에서는 이러한 통계량 추정부터 모델링을 하는 과정까지 구체적으로 살펴보고자 합니다. 모델링을 설명하는 과정에서 ‘order of integration’이라는 개념이 새롭게 등장하는데요. 이를 알게 되면 part.1 도입부에서 언급한 ‘cointegration’이라는 개념을 이해할 수 있게 되므로, 마지막에 cointegration에 대해서도 짧게 짚어본 후, 시계열 분석 글을 마무리하고자 합니다.
사실상 시계열 분석 과목에서 미래값 예측 등을 포함해 중요한 부분들이 더 남아 있지만, 이 시리즈를 통해 가장 기초가 되는 내용은 어느정도 설명이 되었다고 생각해 이후 포스팅에서는 페어트레이딩에서의 cointegration에 좀 더 중점을 두어볼까 합니다. 본 글에서 다루지 않는 부분에 대해서는 하단의 참고자료가 많은 도움이 될 수 있으니, 한 번 확인해보시면 좋을 것 같습니다.
그럼 지금부터 통계량 추정에 대해 알아보겠습니다!
1. Estimation of statistics
미지의 확률 분포 $p(x)$에서 독립적으로 추출된 표본 $a_1, a_2, … , a_n$이 있고, $p(x)$의 기댓값 $E[x]$을 계산하려고 하는 상황을 생각해봅시다. 기댓값의 이론적 정의는
$ E[x]=\int xp(x)dx $
이기 때문에, $p(x)$를 알지 못하는 이상 정확한 기댓값은 구할 수가 없고 추정을 해야 합니다. 이 때, 우리는 보통 $p(x)$에 대한 추정 $\hat{p}(x)$을 추출된 표본을 바탕으로 아래와 같이 정하게 됩니다.
$ \hat{p}(x) = \frac{1}{n} (\delta(x-a_1)+\cdots+\delta(x-a_n)) $
여기서 $\delta(x)$는 dirac delta function입니다. 쉽게 말해 $a_1,…,a_n$이 각각 $1/n$의 확률로 추출되는 분포로 $p(x)$를 추측하겠다는 뜻이죠. 이제 기댓값의 정의에서 $p(x)$ 대신 $\hat{p}(x)$를 이용하여 기댓값을 추정하면 우리가 알고있던 표본 평균이 나오게 됩니다.
$ \hat{E}(x) = \int x\hat{p}(x)dx = \frac{1}{n}\sum_{i=1}^{n} \int x \delta(x-a_i)dx = \frac{1}{n}\sum_{i=1}^{n} a_i $
다른 방식으로도 생각해 볼 수 있습니다. 확률 분포가 $p(x)$를 따르면서 i.i.d.인 확률 변수 $x_1,…,x_n$가 있다고 합시다. 이제 아래와 같이 새로운 확률 변수를 정의하면,
$ X=\frac{1}{n}\sum_{i=1}^{n} x_i $
$E[X] = \frac {1}{n}\sum_{i=1}^{n} E[x_i] = E[x]$가 되는데요. $\frac{1}{n}\sum_{i=1}^{n} a_i$는 $X$에서 추출된 하나의 표본으로 생각할 수 있으므로, 이를 $E[x]$의 추정값으로 사용하는 것은 unbiased estimation이 됩니다. (혹은 중심극한정리를 생각해도 될 것입니다. 표본 평균 $\frac{1}{n}\sum_{i=1}^{n} a_i$는 평균이 $E[x]$인 정규분포를 따릅니다.)
위와 같은 흐름 외에도 여러 추정방식이 있을 수 있습니다. 추정 방식에 따라서는 같은 대상을 추정하더라도 그 값이 달라질 수 있습니다. 즉, 우리는 통계량의 정의와는 별개로 시계열 분석에서는 추정이 어떻게 이루어지는지 알 필요가 있는 것입니다.
특히 일반적인 시계열 데이터 $\{a_t\}_{t=1,…,n}$는 서로 다른 확률 분포 $p(x_t) (t=1,…,n)$에서 한 번씩 추출된 값들의 나열이기 때문에, 위의 예시처럼 하나의 확률 분포에서 여러 개의 표본을 얻은 상황이 아닙니다. 따라서, 시계열 분석에서는 stationary process에서 추출된 시계열 데이터로 가정하고 통계량 추정을 하게 됩니다. 즉, 기댓값 추정의 경우에는 $a_t$를 만들어내는 확률 분포 $p(x_t)$가 $t$에 상관없이 기댓값이 일정하다는 가정하에,
$ E(x_t)=\frac{1}{n}\sum_{i=1}^{n} a_i \quad \quad \forall t \in \mathbb{Z} $
로 추정합니다. 이러한 가정하에 다른 통계량을 추정하게 되고, 유의미한 결과를 얻었을 경우 우리는 stationary process로 모델링에 들어가게 되는 것입니다. 따라서 이어서 소개할 나머지 통계량 추정식들도, stationary process에서 실현된 시계열 데이터라는 가정하에 이루어지는 추정 방식으로 이해하시면 좋을 것 같습니다.
1.1. Estimation
아래의 1.1.1.부터 1.1.4.까지는 $n$개의 시계열 데이터 $\{a_t\}_{t=1,…,n}$를 갖고 있을 때, $\{a_t\}_{t=1,…,n}$을 만들어내는 stationary model $\{x_t\}$이 있다고 하고 notation이 사용되었습니다.
1.1.1. sample mean
$\{x_t\}$의 기댓값 $E[x]$에 대한 추정 $\bar{x}$는 아래와 같이 얻게 됩니다.
$ \bar{x} = \frac{1}{n}(a_1+a_2+\cdots+a_n) $
1.1.2. sample autocovariance
$\{x_t\}$의 autocovariance $\gamma_x(h)$에 대한 추정 $\hat{\gamma}_x(h)$는 아래와 같이 얻게 됩니다.
$ \hat{\gamma}_x(h)=\frac{1}{n} \sum_{t=1}^{n-|h|}(a_{t+|h|}-\bar{x})(a_t-\bar{x}) $
Stationary process의 autocovariance 정의를 보면, $\gamma_x(h)=E[(x_{t+h}-\mu)(x_t-\mu)]$에서 $(x_{t+h}-\mu)(x_t-\mu)$에 대한 기댓값을 취함을 알 수 있는데요. 우리는 정의에 의해 이 기댓값이 $t$에 상관없이 일정하다는 것을 알고 있습니다.
따라서 $t=1,…,n-|h|$에서 각 한 번씩 추출된 $n-|h|$개의 표본 $(a_{1+|h|}-\bar{x})(a_1-\bar{x})$, $(a_{2+|h|}-\bar{x})(a_2-\bar{x})$, $…$ ,$(a_{n}-\bar{x})(a_{n-|h|}-\bar{x})$으로 $(x_{t+h}-\mu)(x_t-\mu)$의 기댓값을 추정하는 것이 일리가 있고, 그 식은 $\frac{1}{n-|h|} \sum_{t=1}^{n-|h|}(a_{t+|h|}-\bar{x})(a_t-\bar{x})$가 될 것입니다.
여기서 unbiased estimation을 유지하면서 $\gamma_x(h)$의 non-negative definite한 성질까지 $\hat{\gamma}_x(h)$에 주기위해 분모가 $n$으로 바뀐 것이 sample autocovariance의 정의가 됩니다.
1.1.3. sample ACF
sample ACF와 sample PACF는 추정된 autocovariance로부터 구하게 되는데요. ACF의 정의와 마찬가지로, sample ACF를 구하는 것이 자연스럽습니다. ACF $\rho_x(h)$의 추정 $\hat{\rho}_x(h)$는 아래와 같이 정의됩니다.
$ \hat{\rho}_x(h)=\frac{\hat{\gamma}_x(h)}{\hat{\gamma}_x(0)} $
1.1.4. sample PACF
sample PACF는 part.1에서 언급한 바와 같이 PACF가 만족하는 관계식을 이용하여 구하게 됩니다. 관계식은 그대로 이용하되, 모든 autocovariance가 sample autocovariance로 바뀌게 됩니다. PACF $\alpha_x(h)$에 대한 추정 $\hat{\alpha}_x(h)$는 아래와 같이 정의되는데요.
$ \hat{\alpha}_x(0)=1 $
$ \hat{\alpha}_x(h)=\hat{\phi}_{hh} \quad \quad (h>0) $
여기서 $\hat{\phi}_{hh}$는 아래 $\hat{\phi}_h$에 대한 관계식에서 나옵니다.
$ \hat{\phi}_h=\hat{\Gamma}_h^{-1} \hat{\gamma}_h $
$ \hat{\phi}_h = \begin{pmatrix} \hat{\phi}_{h1} \\ \hat{\phi}_{h2} \\ \vdots \\ \hat{\phi}_{hh} \end{pmatrix} $
$ \hat{\gamma}_h = \begin{pmatrix} \hat{\gamma}_x(1) \\ \hat{\gamma}_x(2) \\ \vdots \\ \hat{\gamma}_x(h) \end{pmatrix} $
1.2. Background of estimation
지금까지 시계열 데이터가 주어졌을 때, 모델링을 위한 통계량 추정에 대해 살펴 보았습니다. 주어진 시계열 데이터가 stationary process로 모델링이 가능한지 살펴보기 위해, 추정하려는 대상이 stationary process의 통계량이라 간주하고 추정한다는 개념이 바탕에 있었는데요.
이러한 부분이 매끄럽지 않게 느껴지는 분들이 있을 수 있다고 생각합니다. (제가 그랬습니다.) 개인적인 생각으로는 시계열 분석이 현실적인 문제 해결에 초점이 맞춰져있는 점, 추정이나 모델링이 주를 이루는 점 등의 특징을 가지고 있기 때문에, 이론적인 엄밀함보다는 분석 과정에서의 의미를 찾으며 공부를 하는 것이 좋지않을까 합니다.
위에서 말한 부분에 해당하는 경우를 잠시 생각해봅시다. 예를 들어 A회사의 주식데이터 $\{a_t\}_{t=1,…,n}$가 stationary process임을 보이려는 상황을 상상해봅시다. Stationary process의 조건 중 한 가지는 $E(x_t)$가 일정해야 합니다.
이론적으로는, 우리는 매 $t$에 대해 $E(x_t)$에 대한 추정값을 구하고 이것이 일정한 값을 유지하는지 관찰해야 할 것입니다. 그런데 $t$시점에 $E(x_t)$를 추정하기 위해 갖고 있는 데이터가 $a_t$ 하나 밖에 없는 상황입니다. 만약 평행 세계가 있어서 A회사의 주식 데이터가 새로 생성된 것이 있고 그 곳에서 $a’_t$를 얻을 수 있다면 $t$시점의 표본이 늘어나겠지만, 현실은 한 시점에 하나의 데이터만이 존재합니다.
결국 우리는 현실적으로 기댓값이 일정하다는 것을 보일 좋은 방법이 없기 때문에, 일단 stationary process임을 가정하고 $E(x_t)$를 포함한 여러 통계량들을 바로 추정하게 됩니다.
뒤에 모델링 과정을 설명하는 부분에서 다시 나오겠지만, 그 이후 과정 또한 좀 더 생각해 볼까요? 예를 들어 A회사 주식데이터의 통계량 추정 후에 sample ACF 그래프를 보니 lag 3후에 거의 cut off 되는 모양이고, sample PACF 그래프는 exponential하게 감소하는 것으로 간주할 수 있는 모양이 나왔다고 가정해봅시다.
이 경우에는 sample ACF, PACF가 MA(3) process의 ACF, PACF의 특징을 보이기 때문에 MA(3) process로 모델링을 할 수 있게 되는데요. 이렇게 MA(3)로 모델링을 한 후 뒤에서 소개하게 될 잔차 분석이 큰 문제 없이 완료가 되면, $\{a_t\}_{t=1,..,n}$의 stationary process 모델링이 끝나게 됩니다. Stationary process로 모델링을 하는데 그 과정에서 stationary process의 정의는 어디에도 사용되지 않게 되는 것입니다.
단지 ARMA process의 특징(ACF, PACF)을 잘 보이고 잔차 분석이 잘 되었는지 정도를 사용할 뿐입니다. 만약 ACF, PACF가 좋은 모양을 보이지 않는 등의 이유로 ARMA 모델링이 어려워보이는 경우엔, stationary process로 가정한 것을 부정하고 다른 처리 방법을 시도하게 됩니다.
사실 이러한 방법이 정답이 아닐수도 있습니다. (정답이 뭔지 알 방법도 없지만요.) 위에서 $\{a_t\}_{t=1,..,n}$는 non-stationary process에서 생성된 것이어서 통계량 추정부터 MA(3) 모델링이 전부 틀렸지만, 우연히 원하는 결과가 나왔을 가능성도 없지 않습니다.
뒤에서 우리가 배울 여러 모델들 또한 마찬가지입니다. ‘특정 데이터에 대해 어떤 모델을 사용해야한다’ 라던지 ‘이러한 모델을 사용하니 이러한 이유로 성능이 좋았다’와 같은 것들은 이론적으로 보이기가 쉽지 않을 뿐더러, 실용적인 학문은 이런 엄밀함과 별개로 계속 발전해나가는 일이 많습니다.
그러니 앞으로 남은 부분에 대해서도 앞에서와 같이 매끄럽지 않은 부분이 존재할 수 있지만, 이러한 추정과 모델링 과정이 일반적으로 의미가 있어 왔기 때문에 받아들일 가치가 있다고 생각하면 좋을 것 같습니다.
2. Modeling
지금까지 시계열 데이터가 stationary process에서 실현된 것이 맞는지 확인하기 위해 ACF와 PACF를 추정하는 방법에 대해 많은 얘기를 했습니다. 하지만 이는 사실 전체 시계열 분석 과정 중 일부일 뿐입니다. 아직 우리는 stationary process라고 생각되면 어떤 작업을 하는지, non-stationary라 추정되는 데이터는 어떻게 처리하는지 등에 대해 살펴보지 못했습니다.
모든 과정을 전부 자세하게 설명할 수는 없지만, 전체 과정이 어떤 흐름으로 이루어지고 어떤 의미를 갖는지 최대한 소개하도록 하겠습니다.
2.1. General steps of modeling a time series
먼저 우리는 시계열 데이터에 fitting할 모델 $\{x_t\}$를 최종적으로 아래와 같이 구성하기를 원합니다.
$ x_t = m_t + s_t + y_t \quad \quad \forall t \in \mathbb{Z} $
$ where \quad y_t \ \ is \ \ stationary \ \ component \ \ s.t. \ \ E[y_t]=0, $
$ s_t \ \ is \ \ seasonal \ \ component \ \ s.t. \ \ s_{t+d}=s_t, \quad \sum_{j=1}^d s_j =0, $
$ m_t \ \ is \ \ trend \ \ component. $
일반적으로 현실에 존재하는 시계열 데이터는 non-stationary이고 이러한 non-stationarity는 크게 추세(trend)나 주기성(seasonality)으로 나뉩니다. 추세나 주기성은 보통 plotting이나 sample ACF를 통해 그 존재 여부를 확인할 수 있는데요.
시계열 데이터에 추세가 존재하는 경우에는 보통 sample ACF가 cut off되거나 exponential하게 감소하지 않고 아주 느리게 감소하고, 주기성이 있는 데이터의 경우에는 sample ACF도 같은 주기를 갖고 함수값이 요동치게 됩니다.
이렇게 sample ACF를 통해 추세나 주기성이 확인되었다면, 시계열 $x_t$는 추세 성분(trend component) $m_t$와 $d$의 주기를 가진 성분(seasonal component with $d$-period) $s_t$, 그리고 이러한 것들을 제외하고 남은 stationary component $y_t$로 분해되는 과정을 거칩니다. (위에도 나와있지만 일반적으로 stationary component와 seasonal component는 기댓값이 0이 되도록 합니다.)
만약 $m_t$와 $s_t$를 추출한 후 남은 component에 대해 sample ACF가 급감하는 그래프를 보인다면, decomposing이 잘 된것으로 여기고 stationary process로 모델링이 들어가게 되고, 그렇지 않다면 decomposing이 제대로 이루어지지 않은 것이기 때문에 다른 decomposing 방법을 사용하게 됩니다. 특히 앞부분에서 다룬 ACF, PACF를 추정하는 과정은 decomposing후에 $y_t$를 분석하는 과정에 해당되는데요.
이제 전체 스텝을 나열하면 아래와 같습니다.
1) 시계열의 plotting이나 sample ACF 그래프를 살펴본 후 trend나 seasonality가 존재하는지 확인.
2) 존재한다면 trend component $m_t$와 seasonal component $s_t$를 정확히 규명하여(수식으로 표현할 수 있게) 추출. 추출하고 남은 component가 stationary이기를 기대하기 때문에, 만약 남은 component의 sample ACF가 급감하지 않거나 주기성을 가지도록 decomposing된 경우에는 다시 decomposing을 시도.
3) Stationary component로 추정되는 $y_t$에 대해 통계량 추정을 하여 sample ACF와 sample PACF를 그려보고 적당한 order를 갖는 ARMA model 후보들을 선정. 각 model의 parameter 추정.
4) 추정한 ARMA model로 주어진 데이터를 fitting할때 생기는 잔차를 분석(residual analysis). 해당 ARMA model에서 우리에게 주어진 시계열 데이터가 발생하려면 white noise series가 알맞게 실현되어야 하는데 이 값들을 계산한 것을 잔차라고 하고, 이것이 white noise model에서 실현됐다고 추론하는게 타당한지 검증하는 과정을 잔차 분석이라 한다. 여러 후보 model중 잔차분석 등의 여러 결과를 종합하여 가장 적합해 보이는 model을 선택.
5) $y_t$의 ARMA modeling이 잘 완료 되었다면 $x_t$의 modeling을 최종적으로 완성하고, 미래의 데이터에 대해 예측 값과 신뢰구간을 내놓는다(forecasting).
전체 과정을 살펴보시면 앞 단원에서 살펴본 각종 통계량 추정은 3번에 해당하는 부분이었다는 것을 알 수 있습니다. (사실 정확히는 3번 중에서도 model을 선정하는 과정까지만 관련이 있고, model의 parameter를 추정하는 과정은 설명하지 않았는데, 이는 Yule-Walker equation이라는 방정식을 이용하여 해결합니다.)
2번에 해당하는 trend, seasonality 추출에는 moving average smoothing, exponential smoothing, smoothing splines, kernel smoothing, winter method, fourier transform 등의 다양한 고전적인 방법들과 differencing, log 취하기 등의 데이터 변환, 또한 여러 non-stationary modeling 방법들이 있는데, 본 글에서는 고전적 방법들은 제외한 방법들에 집중하려 합니다.
5번에 있는 forecasting에 대한 부분은 바탕이 되는 이론(최대우도추정, 신뢰구간설정)부터, forecasting을 더 빠르고 정확하게 하려는 목적으로 발전된 많은 알고리즘(D-W algorithm, innovation algorithm)까지 많은 내용이 있지만, 본 글의 목적과 벗어나는 내용이 많아 생략하도록 하겠습니다. 4번의 residual analysis에서는 상식으로 알고있으면 도움이 될만한 내용들이 있기 때문에 뒤이어 설명드리려고 합니다.
2.2. Residual analysis of ARMA modeling
이 파트에서는 2.1.의 4번 과정에서 언급된 ‘잔차’라는 것을 실제로 구하고 분석하는 과정을 예시를 들어 설명하려 합니다. 시계열 데이터 $\{a_t\}_{t=1,2,…,n}$ 이 주어져 있고 이를 $x_t = \phi x_{t-1} + \theta \varepsilon_{t-1}+\varepsilon_t$ 인 ARMA(1,1)으로 모델링하려 한다고 가정해봅시다. 만약 parameter $\phi, \theta$에 대한 추정까지 완료가 된 상황이라면, 시계열 데이터가 $\{a_t\}_{t=1,2,…,n}$와 같은 값이 나오도록 $\varepsilon_t$가 아래와 같은 조건식을 만족해야 함을 알 수 있습니다.
$ a_1 = \varepsilon_1 $
$ a_2 = \phi a_1 + \theta \varepsilon_1 + \varepsilon_2 $
$ a_3 = \phi a_2 + \theta \varepsilon_2 + \varepsilon_3 $
즉 위의 식에서 $a_t$는 가지고 있는 데이터고 $\phi, \theta$는 추정이 완료된 값으로써 이미 알고 있는 값이기 때문에, $\varepsilon_t$들을 계산할 수 있고, 이는 white noise model $\{\varepsilon_t\}$이 실제 값으로 실현된 상태라고 생각할 수 있는데요.
이렇게 계산된 시계열을 ‘잔차’라고 부르고, 이 잔차들이 정말 (i.i.d. gaussian) white noise model에서 실현된 값일 가능성이 얼마나 되는지 검증하는 과정을 ‘잔차 분석’이라고 합니다. 잔차 분석에는 여러가지 방법이 있는데 i.i.d. gaussian white noise를 검증하기 위해 사용되는 대표적인 방법 세 가지를 소개하겠습니다.
2.2.1. sample ACF of residual
이론상으로 white noise process는 lag가 0일 때를 제외하고는 ACF가 0이어야 합니다. 하지만 white noise process에서 실현된 시계열 데이터가 주어져 있고, 이것의 sample ACF를 계산했을 때에도 그럴까요?
Sample ACF는 한 번의 실현값으로 ACF를 추정한 것이기 때문에, 위 경우에 white noise의 ACF와 비슷한 모양을 보일 수는 있지만 완벽히 똑같은 건 거의 불가능할 것입니다.
실제로 $\{\varepsilon_t\}$ $\sim$ $iid \ N(0,\sigma^2)$에서 발생한 $n$개의 시계열 데이터에 대해 $\hat{\rho}(h)$의 분포는 $n$이 적당히 크다면 아래와 같습니다.
$ \hat{\rho}(0) = 1 $
$ \hat{\rho}(h) \sim iid \ N(0, \frac{1}{n}) \quad \quad (h>0) $
그렇기 때문에 어떤 시계열 데이터가 i.i.d. gaussian white noise인지 sample ACF를 통해 확인하려면, ‘이 정도면 0이라고 봐도 무방한’ 신뢰구간을 정하고, 0보다 큰 모든 lag에 대해 sample ACF 값이 그 신뢰구간 안에 들어간다면 주어진 데이터는 i.i.d. gaussian white noise일 근거가 있다라고 판단하게 되는 것 입니다.
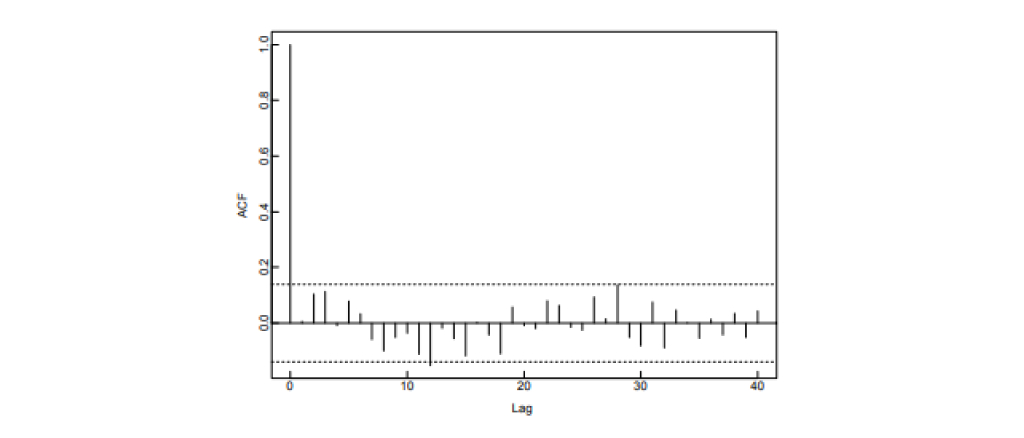
- 출처: Peter J.Brockwell, Richard A. Davis, Introduction to Time Series and Forecasting, second edition.
2.2.2. q-q plot
q-q plot에서 q는 분위수를 뜻하는 quantile의 앞글자로서, 일반적으로 y축은 원하는 확률 분포의 theoretical quantile을, x축은 검정하려는 데이터의 empirical quantile을 plotting한 것을 말합니다. 예를 들어, $1,2,3,4,5$라는 시계열 데이터가 있고 이것이 $N(3, 1^2)$의 분포와 비슷한지 확인하고 싶어 q-q plot을 그린다고 생각해 봅시다.
$1,2,3,4,5$는 각각 전체 데이터의 상위 90%,70%,50%,30%,10%라고 볼 수 있기 때문에 ($1$은 전체 데이터의 상위 80%~100%범위에 있다고 볼 수 있기 때문에 여기서는 90%을 분위수 대푯값으로 정했습니다.) $N(3, 1^2)$에서도 상위 90%,70%,50%,30%,10%에 해당하는 값을 구합니다.
각각 $1.72, 2.48, 3, 3.52, 4.28$로 계산되는데 이제 $1,2,3,4,5$와 순서에 맞게 짝을 맞춰 $(1, 1.72)$, $(2, 2.48)$, $(3, 3)$, $(4, 3.52)$, $(5, 4.28)$ plotting을 한 것이 q-q plot이 되는 것 입니다. (empirical quantile에 해당하는 값이 x축에, theoretical quantile에 해당하는 값이 y축에 오게 했습니다.)
$1,2,3,4,5$가 정말 $N(3, 1^2)$의 분포를 따른다면 q-q plot은 $y=x$ 직선을 보이게 되고, 그렇지 않을수록 $y=x$의 그래프와 괴리가 생기게 됩니다. 예시로 든 경우의 q-q plot은 아래와 같습니다.
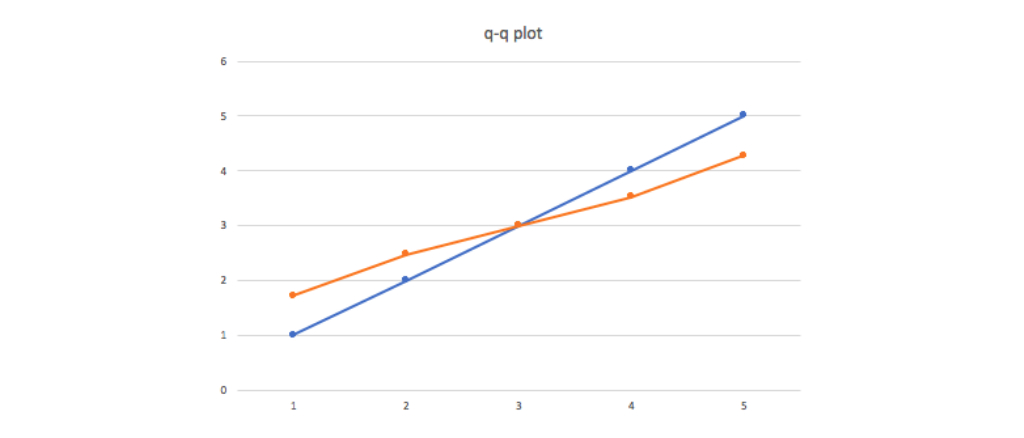
위의 설명에서도 알 수 있듯이, q-q plot은 데이터가 발생한 순서를 고려하지 않기 때문에 시계열 분석의 잔차 분석에서는 반드시 다른 자료들이 함께 사용되어야 할 것입니다. 여기선 다루지 않지만, q-q plot은 모양에 따라 정규분포와 어떤식으로 차이가 있는지 알 수 있기 때문에 추가로 알아두시면 좋을 것 같습니다.
다시 잔차 분석으로 돌아와서, 잔차가 gaussian 분포를 따르는지 검증하려는 상황을 생각해봅시다. 비교하려는 gaussian 분포를 먼저 알아야하기 때문에, 시계열 데이터에서 얻어진 잔차들로부터 평균 $\mu$와 표준편차 $\sigma$를 먼저 구해야할 것입니다. 이제 $N(\mu, \sigma^2)$의 확률 분포와 q-q plot을 그려 $y=x$ 직선과 비교하여 얼마나 차이가 있는지 확인하면 됩니다.
2.2.3. Ljung-Box test, Box-Pierce test
Ljung-Box test, Box-Pierce test는 일종의 카이제곱 테스트입니다. 앞에서 white noise model에서 실현된 시계열 데이터의 경우에는 sample ACF가 평균 0, 표준편차 $1/\sqrt{n}$를 갖는 정규 분포를 따라야 한다고 했습니다.
Ljung-Box test와 Box-Pierce test는 여기에서 좀 더 나아가는데요. Sample ACF의 제곱합과 관련한 통계량을 정의하고(Q statistic이라 부릅니다.), 이 통계량이 특정 카이제곱 분포를 따라야 한다는 수식적 근거에 기반하여 white noise model에서 실현된 시계열일 가능성이 높은지 검정하게 됩니다.
두 test는 통계량의 정의방식에 약간의 차이가 있을 뿐, 정성적으로 시계열 데이터들이 i.i.d. gaussian noise로 간주할 수 있을 정도로 (시점에) 독립적인 모습을 보이고 있는지 확인한다는 점에서 비슷한 방식입니다. 두 test 모두 각자의 Q 통계량 값이 높을수록 카이제곱 분포에서 흔하지 않은 경우이고, 따라서 이 경우 white noise일 가능성이 적은 쪽에 무게를 두게 됩니다. 참고로 각각의 Q 통계량에 대한 정의는 아래와 같습니다.
$ Q_h=n(n+2) \sum_{k=1}^h \frac{\hat{\rho}(k)^2}{n-k} \quad for \quad Ljung-Box \quad test $
$ Q_h=n \sum_{k=1}^h \hat{\rho}(k)^2 \quad for \quad Box-Pierce \quad test $
아래는 통계프로그램 R을 사용하여 특정 시계열 데이터에 대해 ARMA modeling을 한 후, 잔차를 분석하는 화면입니다. 첫 번째는 잔차를 직접 plotting한 것이고, 이어서 순서대로 sample ACF, q-q plot, Ljung-Box test에 관한 자료가 있음을 확인할 수 있습니다.
마지막 Ljung-Box test를 나타내는 그림을 살펴보면 x축은 lag, y축은 p-value를 나타내는데요. 일반적으로 p-value가 낮은 것이 $Q_h$가 큰 값으로 추정됐다는 것을 의미하기 때문에 낮은 p-value들이 관측되는 경우에는 새로운 모델을 찾아보게 됩니다. 즉 모든 lag에 대해 p-value가 높은 경우일수록 잔차가 i.i.d. gaussian noise일 가능성이 높다고 여기기 때문에 그러한 잔차가 나오는 모델을 찾는 것이 좋습니다.
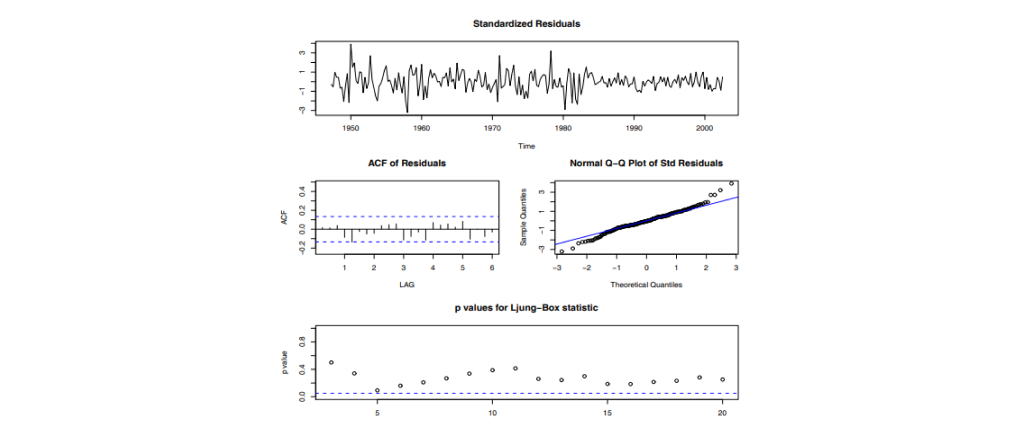
2.3. Dealing with non-stationary process
시계열 모델링을 할 때 trend component, seasonal component를 추출해내고 stationary component만 남기는 decomposing을 먼저 한다고 하였는데, 여러 decomposing 방법 중 differencing에 대해서도 언급했었습니다. 실제로 시계열 데이터가 non-stationary process로 추측되는 경우 여러 방법들 중에 가장 먼저 시도하는 것이 differencing을 하거나 데이터에 log를 취하는 것인데요.
일반적으로 이러한 작업은 취하면 취할수록 데이터가 안정적으로 변환되기 때문입니다. 현실에 존재하는 많은 데이터들이 random walk와 같은 누적형 process이거나(나중에 나오겠지만 이러한 process는 적분 과정 혹은 integrated process라 합니다.),
시간에 따라 exponential하게 변하는 꼴이기 때문에 이러한 방법을 먼저 시도해보는 것이기도 합니다. 만약 모델링에 도움이 되는 데이터에 대한 사전 지식이 있는 경우에는 그것을 이용한 방법을 먼저 적용하는 것이 일반적입니다.
Difference operator & Integrated process
그럼 여기서 잠깐 differencing에 대해 수식으로 정리하고 넘어가겠습니다. 시계열 (모델이나 데이터 모두 해당됩니다.) $x_t$에 대해 differecing을 한 번하여 얻은 새로운 시계열은 $y_t=\nabla x_t$와 같이 표기하고($\Delta x_t$로 표기하기도 합니다.) 아래와 같이 계산된 시계열을 의미합니다.
$ y_t=\nabla x_t = (1-B)x_t = x_t-x_{t-1} $
$B$는 part.1에서 등장했었던 backshift operator입니다(lag operator라고도 합니다). 같은 방식으로 $x_t$를 연속으로 d번 differencing한 시계열 $y_t$는 아래와 같이 구해지는 것을 알 수 있습니다.
$ y_t=\nabla^d x_t = (1-B)^dx_t $
위에서 언급했듯이 시계열 데이터에 log를 취해주거나 differencing을 하여 새로운 시계열을 얻을수록, 데이터는 scale이 줄어들며 stationary process로 모델링하기 좋은 안정한 행태를 보이게 되는데요. 만약 어떤 시계열 모델 $\{x_t\}$가 d번 differencing을 해서 stationary해진다면 이러한 process는 ‘integrated of order d 이다(d차 적분 과정이다)’ 혹은 ‘order of integration이 d인 시계열이다(적분 차수가 d인 시계열이다)’라고 표현합니다. Stationary process는 order of integration이 0인 과정이라 생각하면 될 것 같습니다.
2.3.1. ARIMA
보통 시계열 데이터는 non-stationary한 경우가 많고(stationary process로 모델링이 안되는 경우가 많고), 이에 대한 가장 대표적인 해결 방법은 differencing을 한 후 stationary process로 모델링하는 것이라 하였습니다.
2.1.에서 전체 모델링 과정을 소개할 때 3번에서도 언급하였지만, stationary process로 모델링을 하는 것은 곧 ARMA model로 fitting하는 것을 말합니다. 따라서 differencing을 d번한 후 ARMA 모델링을 하는 것은, 시계열 모델 $x_t$에 대해 $(1-B)^d x_t$가 ARMA process임을 말하고, 다시 말해 우리가 사용하려는 모델 $x_t$가 아래의 조건을 만족함을 알 수 있습니다.
$ (1-\phi_1 B-\cdots-\phi_p B^p)(1-B)^dx_t=(1+\theta_1 B+\cdots+\theta_q B^q)\varepsilon_t $
위의 식에서 디테일한 조건들을 언급하진 않았는데, $\phi(B)=1-\phi_1 B-\cdots-\phi_p B^p$, $\theta(B)=1+\theta_1 B+\cdots+\theta_q B^q$는 각각 autoregressive operator, moving-average operator로써 $(1-B)^dx_t$가 (causal) ARMA process가 됨을 의미한다고 받아들이시면 어떤 조건들이 생략되어 있는지 알 수 있을것이라 생각합니다. 그리고 이 때 $x_t$를 ARIMA(p,d,q) process(autoregressive integrated moving average process) 라고 합니다.
일반적으로 differencing의 횟수 d가 높아질수록 stationary한 모습에 가까워지기 때문에 d를 높게 잡을수록 ARIMA로 fitting될 가능성이 높습니다. 하지만 그럴 경우 ARIMA model식이 너무 복잡해져 데이터에 overfitting된 모델이 나올 경향이 크기 때문에, 보통 d가 2보다 큰 ARIMA 모델을 사용해야할 경우엔 다른 모델을 찾는 것이 좋습니다.
또한 두 개 이상의 ARIMA model로 fitting이 가능할 때에는, 가급적 d가 작은 ARIMA model을 사용하는 것이 좋은데요. 이것은 differencing을 많이 하는 경우 오히려 fitting에 필요한 파라미터가 늘어나는 일이 많기 때문입니다.
예를 들어 random walk process $x_t-x_{t-1}=\varepsilon_t$에서 발생한 데이터를 생각해봅시다. 이 경우 $x_t$에 differencing을 한 번만 하면 white noise이기 때문에, 데이터를 한 번만 differencing하면 stationary modeling이 가능할 것입니다.
그런데 두 번 differencing을 시행한 경우에도 $\nabla^2 x_t = \varepsilon_t-\varepsilon_{t-1}$이기 때문에, 데이터를 두 번 differencing을 한 것 또한 stationary modeling이 가능한데 이 경우 데이터는 $\varepsilon_t-\varepsilon_{t-1}$와 같은 MA(1) model을 따를 것 이기 때문에 처음보다 추정해야할 parameter가 하나 증가하게 됩니다.
다시 말해, 데이터를 한 번만 differencing 했을 경우에는 sample ACF를 그려보면 white noise와 같은 모양을 보일 것이기 때문에 $\nabla x_t = \varepsilon_t$으로 모델링을 끝내면 되는데, 두 번 differencing한 경우에는 sample ACF가 MA(1)과 같은 모양을 보이므로 $\nabla^2 x_t = \varepsilon_t + \theta \varepsilon_{t-1}$에서 $\theta$라는 파라미터를 추정해야하는 번거로움이 생기게 되는 것입니다.
이러한 현상 또한 데이터에 overfitting되는 모델을 찾게 하는 효과를 주고, 따라서 differencing을 너무 많이 하는 것은 좋지 않다는 것을 인지하고 있어야 합니다.
Unit Root test
지금까지 배운 바로는 시계열 데이터가 non-stationary로 추정될 때, differencing을 하였을 경우 stationary process로 모델링이 가능한지 바로 알 수 있는 방법은 없었습니다. ACF, PACF 추정과 residual analysis등을 시행해봐야 알 수 있었고, 만약 결과가 적합하지 않다면 추가로 differencing을 해봐야하는 사태가 발생합니다.
Unit Root test(단위근 검정) 는 이것을 한 번에 알 수 있게 하는 검정법인데요. 현재 상태가 stationary인지, differencing을 한 번하면 stationary하게 되는지, differencing을 두 번하면 stationary하게 되는지에 대한 정보를 제공합니다. (보통 differencing을 세 번 이상으로 해보는 경우는 잘 없기 때문에 이 정도의 검정만 존재하는 것 같습니다.)
데이터의 형태가 exponential하거나 양,음 값을 진동하는 등의 특이한 경우에는 굳이 differencing을 몇 번해야 stationary하게 되는지 검사해볼 필요가 없기 때문에, 주로 integrated process로 보이는 데이터에 대해 적용하는 검정 방법입니다.
실제로 경제 지표, 주식 데이터 등이 integrated process의 대표적 예시들인 만큼, 이 분야에서 많이 사용되고 있고 이러한 데이터들에 대해 cointegration test(공적분 검정)를 할 때에도 이용되고 있습니다.
2.3.2. Other non-stationary models
ARIMA model 이외에도 다양한 non-stationary model들이 존재하는데, 그 중 대표적인 것 몇 개만 소개합니다.
SARIMA
SARIMA model은 seasonal ARIMA model을 줄인것으로, ARIMA로 커버하기 힘든 seasonality까지 고려된 ARIMA의 발전된 형태인데요. 먼저 정의는 아래와 같습니다.
$ \phi(B)\Phi(B^s)\nabla^d\nabla_s^Dx_t = \theta(B)\Theta(B^s)\varepsilon_t $
$ \phi(B)=1-\phi_1 B-\cdots-\phi_p B^p $
$ \Phi(B)=1-\Phi_1 B-\cdots-\Phi_P B^P $
$ \nabla = (1-B) $
$ \nabla_s = (1-B^s) $
$ \theta(B)=1+\theta_1 B+\cdots+\theta_q B^q $
$ \Theta(B)=1+\Theta_1 B+\cdots+\Theta_Q B^Q $
정의는 복잡하지만 한 단계씩 생각하면 이해하기 어렵지 않습니다. 먼저 ARIMA(P,D,Q) process를 생각하면 아래와 같은데,
$ \Phi(B)\nabla^Dx_t = \Theta(B)\varepsilon_t $
이러한 과정이 $s$의 시간 간격씩 건너뛰며 진행된다고 하면 우리는 위의 조건식에서 $B$대신 $B^s$로 바꿔 표현해야 할 것입니다. 즉 아래와 같이 가장 기본적인 $s$-period ARIMA(P,D,Q) process를 적을 수 있습니다.
$ \Phi(B^s)\nabla_s^Dx_t = \Theta(B^s)\varepsilon_t $
$s$-period ARIMA process라는 명칭은 정식 명칭이 아니지만, 위와 같은 조건을 만족하는 과정이 보통 첫 $s$개의 시계열 패턴이 주기적으로 반복되는 형태를 보이기 때문에 그렇게 명명하였는데요.
위 식을 변형하여 이 패턴이 단순히 반복되는 것이 아닌 추세를 갖고 반복되는 경우까지 고려할 수가 있습니다. 바로 ARIMA(p,d,q) process의 조건식
$ \phi(B)\nabla^dx_t = \theta(B)\varepsilon_t $
에서 좌변의 항을 위의 $s$-period ARIMA(P,D,Q) process에서 $x_t$자리에, 우변의 항을 $\varepsilon_t$ 자리에 대체하여 넣으면 되는데요. 그렇게하면 우리는 SARIMA model의 일반적인 형태를 얻게 됩니다. 우리는 이러한 process에 대해 order를 포함하여 SARIMA$(p,d,q)\times(P,D,Q)_s$ process (with period $s$) 라고 부릅니다.
쉽게 이해하자면, ARIMA model은 $y=x$와 같은 trend line에 noise가 섞인 유형의 시계열에 대해 적용 가능한 모델이고, SARIMA model은 $y=x$대신 $y=x+\sin x$와 같이 trend와 seasonality가 함께있는 경우에도 적용가능한 모델이라 생각하면 좋을 것 같습니다.
ARFIMA
ARFIMA는 ARIMA의 변형모델로서, differencing을 아무리 많이해도 trend가 남아있고, stationary 가 되지 않는 시계열에 대해 적용 가능한 모델입니다. 앞에서 몇 번 언급하였듯이 stationary 시계열은 ACF가 급감하는 그래프를 보이는데, lag가 아무리 커져도 천천히 감소만 할 뿐 0근처에도 가지않는 ACF를 가진 시계열의 경우 보통 ARFIMA를 통해 모델링을 합니다.
ARFIMA의 FI는 Fractional Integrated의 첫글자로써, ARIMA model과 조건식이 동일하지만 $(1-B)^d$의 $d$가 $0<|d|<0.5$와 같이 유리수(fractional) 범위에서 거듭제곱이 된 형태이기 때문에 만들어진 이름인데요. Fractionally integrated ARMA process, ARFIMA(p,d,q) process 등으로 다양하게 불리고 있습니다.
ARFIMA model의 경우에는 유리수의 거듭제곱으로 인해 $x_t$의 조건식이 무한급수의 형태로 표현되는데요. 이러한 성질로 인해 ACF의 값을 lag에 따라 계속 더해도 수렴하지않고 무한대로 발산한다는 것이 증명되어 있고, 따라서 앞서 말한 유형의 시계열에 적용되고 있습니다. ARFIMA의 조건식은 ARIMA와 동일하기 때문에 수식 정의는 생략하고 넘어가도록 하겠습니다.
ARCH
ARCH는 AR model에서 white noise의 부분에 변형이 들어간 모델입니다. ARCH의 모델은 주식의 변동성(volatility) 그래프를 모델링하기 위해 처음 고안되었는데, 전체적으로 trend나 seasonality는 없어보여도 noise의 크기가 커졌다 줄어들었다 하는 것 같은 모양의 데이터에 대해 기존의 방법으로 모델링을 할 수 없게 되었기 때문입니다.
ARCH(p) process (autoregressive conditional heteroscedasticity 의 약자입니다.) $x_t$는 아래와 같이 정의됩니다.
$ \varepsilon_t \sim iid \ N(0,1) $
$ x_t = \sigma_t \varepsilon_t $
$ \sigma_t^2 = \alpha_0 + \sum_{i=1}^p \alpha_i x_{t-i}^2 $
약간의 계산을 통해 $x_t$가 white noise의 조건을 만족하는 것을 알 수 있는데요. 이러한 성질과 위의 조건식을 통해, ARCH process는 이전 값들의 영향을 받으며, noise의 크기가 변하는 과정을 의미함을 알 수 있습니다.
3. Multivariate model
본 파트는 시계열 분석의 핵심 흐름에서 꼭 필요한 부분은 아니지만, 지금까지 설명한 것을 바탕으로 페어트레이딩에서 쓰이는 cointegration의 개념을 소개해드릴 수 있게 되어 마련한 단원입니다. 어려운 개념이지만 VAR과 함께 간단히 짚고 넘어가려고 합니다.
3.1. VAR
VAR model은 vector autoregressive model의 줄임말로서, 기존 model들의 multivariate 버전을 가리키는 것이라 생각하시면 됩니다. Multivariate ARMA model등의 이름이 조금 더 포괄적인 표현이긴 하지만, VAR 또한 multivariate time series를 가리키는 말로 많이 사용됩니다.
VAR model은 쉽게 말해 지금까지 논의했던 것들이 $x_t=(x_{1t},x_{2t},\ldots,x_{nt})^T$와 같이 n차원의 시계열에 대해 적용되는 것인데요. 사실 실제로는 VAR은 차원의 차이만 있다고 생각하기엔 조금 더 까다로운 내용들이 있습니다.
예를 들어 $\{x_t\}$의 correlation을 계산할 때도, 한 시계열 $\{x_{1t}\}$ 안에서 두 시점에 대해 correlation만 따지면 안되고($\{x_{1t}\}$의 ACF), 서로 다른 두 시계열에서 하나의 시점씩을 선택해 계산할 수 있는 correlation도 따져봐야 하기 때문입니다(예를 들어 $x_{1t}$와 $x_{2(t+h)}$의 correlation).
(우리는 뒤의 correlation을 cross-correlation이라 합니다.) 따라서 stationarity와 correlation function의 정의 등이 조금 더 복잡하게 변하게 됩니다. 간단하게는, VAR model에서는 서로 다른 두 시계열끼리 영향을 주는 것도 modeling안에 포함되기 때문에 복잡해지는 것으로 생각하면 됩니다.
이제 VAR에서 differencing을 하는 상황을 상상해봅시다. 만약 시계열 $\{x_t\}$의 첫번째 성분 $\{x_{1t}\}$부터 $n$번째 성분 $\{x_{nt}\}$까지 모두 integrated of order 1의 상태라면 $x_t=(x_{1t},x_{2t},\ldots,x_{nt})^T$를 differencing해서 modeling하는 것은 굉장히 효율적일 것 입니다.
그런데 만약 $\{x_{1t}\}$부터 $\{x_{nt}\}$가 공통적인 non-stationary series에(order of integrated가 1인) additional term이 더해진 방식으로 생성된 시계열이라면, 단순히 $x_t$에 differencing을 적용하는 것은 비효율적일 수 있습니다.
앞에서도 언급했지만, differencing을 불필요하게 과하게 하는 경우에는 parameter가 필요 이상으로 많아져 model이 데이터에 overfitting될 수 있기 때문입니다. 이런 경우에 필요한 개념이 바로 cointegration입니다.
3.2. Cointegration
VAR model $\{x_t=(x_{1t},x_{2t},\ldots,x_{nt})^T\}_{t=1,2,\ldots}$에서 $x_{1t},\ldots, x_{nt}$가 동일하게 integrated of order $d$상태이고 이들의 적절한 선형결합 $\alpha_1x_{1t}+\alpha_2x_{2t}+\cdots+\alpha_nx_{nt}(=\boldsymbol{\alpha}^Tx_t)$이 integrated of order $d’$ ($d’<d$)가 될 경우 $x_{1t},\ldots, x_{nt}$는 ‘cointegrated (with cointegration vector $\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_n)^T$) 되있다’ 혹은 ‘cointegration 관계에 있다’고 합니다. 2차원 시계열 $x_t=(x_{1t}, x_{2t})^T$로 예를 들어봅시다.
$ x_{1t}=\sum_{j=1}^{t} \varepsilon_j \quad \quad \{\varepsilon_t\} \sim iid\ N(0,\sigma^2) $
$ x_{2t}=x_{1t}+\eta_t \quad \quad \{\eta_t\} \sim iid\ N(0,\tau^2) $
$ (\ \{\eta_t\} \; is \; independent \; of \; \{\varepsilon_t\}\ ) $
위와 같은 조건을 만족하는 시계열 $x_t=(x_{1t}, x_{2t})^T$을 살펴봅시다. $x_{1t}$와 $x_{2t}$는 둘 다 integrated of order 1인데 $x_{1t}-x_{2t}=\eta_t$는 integrated of order 0(stationary)이므로 둘은 cointegration 관계에 있음을 알 수 있습니다. (cointegration vector 는 $\boldsymbol{\alpha}=(1,-1)^T$가 됩니다.)
만약 위와 같은 cointegration 관계가 있는 시계열 데이터가 있다면, $x_{1t}$에 대한 모델링을 먼저 마친 후 $\eta_t$만큼을 추가해 $x_{2t}$를 모델링하면 될 것입니다. 그런데 만약 cointegration 관계를 신경쓰지 않고 모델링을 하게되면 어떻게 될까요? $x_t=(x_{1t}, x_{2t})^T$에 differencing을 한 시계열 $\nabla x_t =(u_{1t}, u_{2t})^T$를 생각해봅시다.
$ u_{1t} = \varepsilon_t $
$ u_{2t} = \varepsilon_t + \eta_t - \eta_{t-1} $
이 경우 $u_{1t}, u_{2t}$는 모두 stationary해졌지만 $u_{2t}$의 경우에는 추정해야할 parameter가 더 늘어나게 되어 모델링이 더 복잡해짐을 알 수 있습니다. 따라서 여러 시계열이 non-stationary component를 공유함으로 인해 함께 움직이게 되는 경우에는 cointegration 개념을 이용하는 것이 유용한데요.
특히 주식 데이터는 보통 order of integration이 1인 process를 따르는 것으로 알려져 있어, cointegration 관계에 있는 주식들의 경우에는 적절한 선형결합을 하는 경우 order of integration이 0인 stationary process가 되어 유용하게 쓰일 수 있습니다.
만약 위의 예시처럼 두 주식 $x_{1t}$, $x_{2t}$가 cointegrated 되어 있고 cointegration coefficient가 $(1, -1)$이라면 $x_{1t}$주식을 1주 long하고 $x_{2t}$주식을 1주 short한 포트폴리오는 stationary process를 따르게 되기 때문에 통계적 차익 거래에 이용할 수 있게되는 것입니다. 주식 데이터 이외에 다른 가격 데이터나 경제 지표들도 cointegration 분석이 많이 이용되고 있습니다.
시계열 데이터들에 cointegration 관계가 존재하는지 검정하는 cointegration test에는 여러 가지 방법이 있는데요. 간단한 예시로는 Engle-Granger test로써, 두 시계열 데이터 $\{x_{t}\},\{y_{t}\}$가 있을 때 $x_t$에 $y_t$를 선형회귀 시킨 후 잔차에 대해 unit root test를 시행하여 stationarity 검사를 하는 방법이 있습니다. 위에서 예시를 들었던 $x_{1t},x_{2t}$의 경우에는,
$ x_{2t}=x_{1t}+\eta_t \quad \rightarrow \quad x_{1t}=x_{2t}-\eta_t $
의 관계식을 통해 선형회귀 계수가 1이 되고 잔차는 $-\eta_t$가 됨을 알 수 있는데요. $\{-\eta_t\}$에 대해 unit root test를 시행하면 stationary process로 추정될 것이기 때문에, 이를 통해 두 데이터가 현재 non-stationary process를 공유하고 있고, 적절히 선형결합을 하면 이러한 non-stationary component는 사라지고 stationary한 잔차만 남게할 수 있음을 추측할 수 있습니다.
즉 cointegration 관계를 발견하게 되는 것이죠. 하지만 이러한 Engle-Granger test는 시계열 데이터가 두 개여야 선형회귀가 쉽고, unit root test로는 order of integration이 0,1,2인 것 정도만 잡아내는 한계가 있기 때문에, 상황에 따라 더 정확하고 많은 경우에 검증할 수 있는 Johanson test라는 검증법이 사용되기도 합니다.
4. Conclusion
이번 편에서는 데이터를 모델링을 하는 전체적인 과정과 앞의 글에서 다루지 못했던 non-stationary model들에 대해서 알아보았습니다. 앞에서도 몇 번 언급하였듯이, part.1, 2에서 다룬 내용이 시계열 분석의 전부는 아닙니다.
Yule-Walker equation, forecasting과 같이 중요한 개념이지만, 이 글에서 다루고 있지 않은 것들도 있는데요. 시계열 분석 과정을 이해할 때 혹은 기본적으로 시계열 데이터들을 다룰 때 필요한 개념들에 대해 집중했기 때문에, 오히려 시계열 분석을 한 흐름에 이해하기에 더 도움이 되지 않을까 생각합니다.
더불어 페어트레이딩에 관심이 있는데 cointegration이라는 개념이 복잡해 접근하지 못하셨던 분들을 위해서도, 빠르게 개념에 접근할 수 있는 기회가 되었으면 좋겠습니다.
이후의 포스팅에서는 드디어 페어트레이딩으로 들어가서, 페어를 찾는 과정 및 cointegration test가 어떤 역할을 하는지 알아볼 예정입니다. 또한 개인적으로, 실제 페어트레이딩에서는 cointegration 개념을 알고 검정을 하는 것만으로 바로 좋은 수익을 낼 수 있는 것이 아니기 때문에, 이를 개선하기 위해 어떠한 시도를 할 수 있는지에 대해서도 연구를 해볼 계획입니다.
의미있는 결과들이 나온다면 이 또한 포스팅을 이어갈 예정입니다. 읽어주셔서 감사합니다.
참고문헌
[1] 시계열 분석 강의 - 이기천 교수
[2] Robert H.Shumway, David S. Stoffer, Time Series Analysis and Its Applications, fourth edition.
[3] Peter J.Brockwell, Richard A. Davis, Introduction to Time Series and Forecasting, second edition.