안녕하세요. 이스트소프트 A.I. PLUS Lab입니다. 이번 포스팅에서는 머신러닝의 학습 방법 중 하나인 준지도학습(semi-supervised learning, SSL)에 대해 다루어보려고 합니다.

SSL 자체가 워낙 거대한 주제이기 때문에 이번 포스트에서 전체적인 내용을 모두 다루기보다, 일부 방법론과 각 방법론에서 읽어 볼만한 주요 논문들을 소개하려고 합니다. 전체적인 흐름은 레퍼런스 [2]의 내용에 기반하고 있기 때문에 SSL 연구를 위해 자세한 기반 지식이 필요하신 분들은 아래 레퍼런스를 참고하시면 좋을 것 같습니다.

머신러닝 학습 방법의 구분: 지도학습, 비지도학습, 준지도학습

머신러닝의 학습 방법은 크게 지도학습(supervised learning, SL)과 비지도학습(unsupervised learning, UL)으로 나뉘는데요. 이 둘을 나누는 기준은 바로 학습 데이터의 라벨(label) 유무입니다.

먼저 지도학습은 정답이 되는 데이터(labeled data)를 학습시켜 새로운 입력(input) 데이터가 무엇인지 예측하는 것을 목표로 진행되는데요. 지도학습은 크게 분류(classification)과 회귀(regression)으로 나뉩니다. 이에 반해 비지도학습은 정답지 없이 주어진 입력 데이터 간의 숨어있는 구조를 찾아 비슷한 데이터끼리 묶는 것(clustering)을 목표로 합니다.

이 외에 지도학습과 비지도학습의 조합으로 이루어진 준지도학습이 있습니다. 준지도학습의 이름에는 절반을 뜻하는 ‘semi-’가 붙지만, 실제로 이 학습방식에는 위에서 언급한 레이블링된 데이터와 레이블링되지 않는 데이터가 모두 사용됩니다. 준지도학습에서는 한 쪽의 데이터에 있는 추가 정보를 활용해 다른 데이터 학습에서의 성능을 높이는 것을 목표로 하는데요. 분류 분야를 보면 기존 지도학습 데이터에 레이블링되지 않은 데이터 정보를 추가로 사용해 성능을 향상시키고, 클러스터링 분야에서는 새로운 데이터를 어느 클러스터에 넣을지 결정함에 있어 도움을 받을 수 있습니다.

그림 1은 이런 데이터 사용 측면에서 지도학습과 준지도학습, 비지도학습의 성격 차이를 보여줍니다. 보시면 준지도학습에서는 위에서 이야기한것처럼 두 종류의 데이터를 전부 사용하고 있습니다.

Semi-supervised learning의 필요성

왜 준지도학습이 필요하게 되었을까요? 준지도학습은 바로 정답 데이터를 수집하는 ‘데이터 레이블링’ 작업에 소요되는 많은 자원과 비용 때문에 등장하게 되었습니다.

지금까지 딥러닝은 많은 분류 문제에서 좋은 성능을 보여줬고, 이 문제를 해결하기 위해 데이터 레이블링 작업이 필수적으로 수반되어 왔습니다. 초기 딥러닝은 ‘손글씨 인식’, ‘사진의 물체 인식’ 등 비교적 단순한 문제를 다뤘기 때문에 전문가가 아닌 사람들도 쉽게 레이블링 작업을 수행할 수 있었고, 이에 대한 작업 결과도 명확해 큰 문제가 되지 않았습니다.

하지만, 최근 딥러닝이 다루는 문제가 복잡해지고 응용 분야가 다양해지면서 레이블링 작업 자체가 하나의 문제로 떠올랐는데요. 추상적인 문제를 해결하기 위해 그 판단 기준을 새롭게 세워야 하거나, 전문 지식을 필요로 하는 문제를 해결하기 위해 해당 분야의 전문가가 필요해지는 등 레이블링 작업에 드는 시간과 비용이 증가하게 된 것입니다.

예를 들어 ‘사진 속 인물의 감정’에 대한 레이블링은 ‘감정’이란 추상적인 부분을 다루기 때문에 ‘사진 속 대상이 무엇인지’에 대한 레이블링보다 그 결과 기준이 애매해지게 되는데요. 많은 사람들이 동의할 수 있는 작업 결과를 만들기 위해서는 그 기준이 새롭게 세워야겠죠? 또한, AI 스피커 또는 번역 플랫폼 개발 등 다양한 문제에 많이 활용되는 ‘말뭉치(corpus, 코퍼스)’를 만들기 위해서는 언어학 전문가들이 필요하게 되는데요. 이 외에도 수많은 견종, 식물 등을 레이블링 하기 위해서는 다양한 전문 지식을 가진 사람들이 필요하게 됩니다.

이와 같은 이유로 단순히 작업하는 사람만을 늘려 레이블링 문제를 해결하기에는 무리가 있기 때문에 ‘준지도학습’이 등장하게 되었습니다. 특히 위에서 언급했던 응용 분야에서는 레이블이 없는 데이터는 비교적 구하기 쉬운 경우가 많기 때문에, 준지도학습은 레이블된 데이터가 적을 때 레이블이 없는 데이터를 사용해 분류기의 성능을 향상시키는 것을 목표로 많이 활용되고 있습니다.

Assumptions of SSL

SSL은 위에서 언급한 대로 기존 SL 모델의 성능을 올려줄 수 있지만, 항상 그런 것은 아닙니다. 레이블되지 않은 데이터가 의미 있게 사용되기 위해서는 데이터 분포에 대한 몇 가지 가정이 필요합니다. 또한 SSL을 위한 다양한 접근 방법들이 있는데, 이런 방법들은 명시적/묵시적으로 이런 가정들에 기반한 접근을 하고 있습니다. 가정들의 정확한 분류는 논문에 따라 약간의 차이가 있긴 하지만 핵심적인 내용은 거의 비슷합니다.

그 첫 번째는 (semi-supervised) smoothness 가정입니다. Smoothness 가정은 확률 밀도가 높은 지역의 입력값 $ x_1, x_2 $가 가깝다면, 각각에 연관된 레이블 $ y_1, y_2 $도 그래야 한다는 것입니다. SSL에서는 이 가정을 레이블이 없는 데이터에도 적용하여 $ x_1 $이 레이블이 있는 데이터고 $ x_2, x_3$이 레이블이 없는 데이터일 때, $ x_1 $이 $ x_2 $와 가깝고, $ x_2 $ 와 $ x_3 $가 가깝다면 $ x_1 $이 $ x_3 $와 가깝지 않더라도 $ x_3 $의 레이블이 $ x_1 $과 같을 것이라고 기대할 수 있습니다.

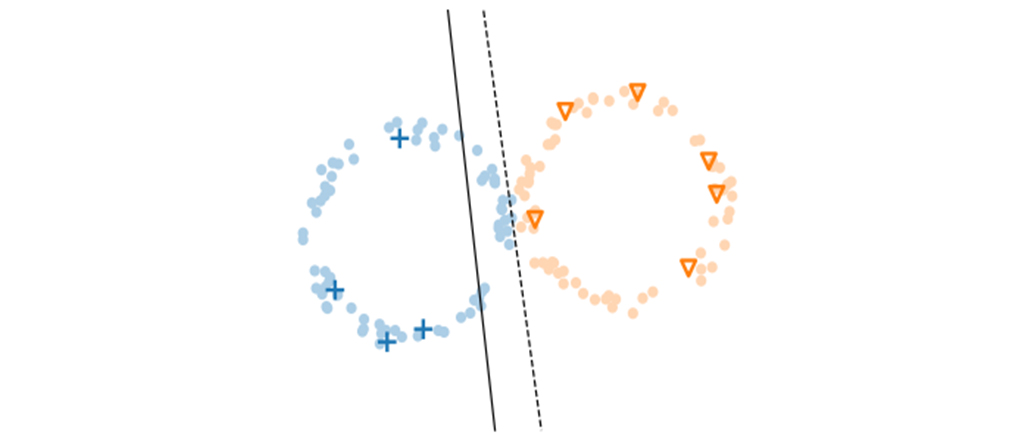
두 번째는 low-density 가정입니다. low-density 가정은 모델의 결정 경계가 데이터의 확률 밀도가 높은 곳을 지나지 않는다는 가정입니다. low-density 가정은 smoothness 가정과 연관성이 있는데, low-density 가정에 따라 모델의 결정 경계를 두면 low-density 지역은 그 주변에 데이터들이 적기 때문에 smoothness 가정을 위반하지 않습니다. 반면에 high-density 지역에는 데이터들이 많이 모여 있을 것이고, 해당 지역에 결정 경계를 놓는다면 가까운 데이터는 같은 레이블을 가진다는 smoothness 가정을 위반하게 됩니다. 그림 2는 이러한 가정들을 통해 만들어지는 결정 경계를 보여주고 있습니다.

세 번째는 manifold 가정입니다. Manifold 가정은 앞의 가정들과 비슷한데, 고차원의 입력 데이터가 저차원 공간에서 특정한 구조[manifold]를 따라 놓여 있다는 것입니다. 이는 입력 데이터가 실제로는 여러 개의 저차원 manifold의 결합으로 이루어져 있다는 것과, 같은 manifold 상의 데이터는 같은 레이블을 가지고 있다는 것을 의미합니다. 또한 manifold 가정은 모델 설계 시에 유용할 수 있습니다. 기존 ML에서 잘 알려진 문제인 차원의 저주(curse of dimensionality)는 데이터가 고차원에 존재할 경우 문제가 될 수 있음을 말하는데, 데이터의 분포에 대해 manifold 가정을 할 경우 실제 관련이 있는 차원상에서 데이터를 다루어야 할 필요가 있으며, 이를 통해 고차원 공간상에서 일어날 수 있는 문제를 피할 수 있습니다.

SSL에서 언급되는 다른 가정으로는 클러스터 가정이 있는데, 클러스터 가정은 데이터들이 같은 클러스터에 속하면 해당 데이터들은 같은 클래스에 속한다는 가정입니다. 클러스터 가정은 위 가정들의 일반화로 볼 수 있는데, 이에 따르면 클러스터링을 할 때 유사도(similarity)를 기준으로 클러스터를 나누게 됩니다. 이때 입력 공간상에서 가까운 것들을 클러스터로 본다면 smoothness 가정이 되고, 확률 밀도가 높은 지역의 데이터 포인트를 클러스터로 본다면 low-density 가정이 되고, 저차원 manifold 상의 데이터 포인트들을 클러스터로 본다면 manifold 가정이 됩니다 [2].

Taxonomy of SSL

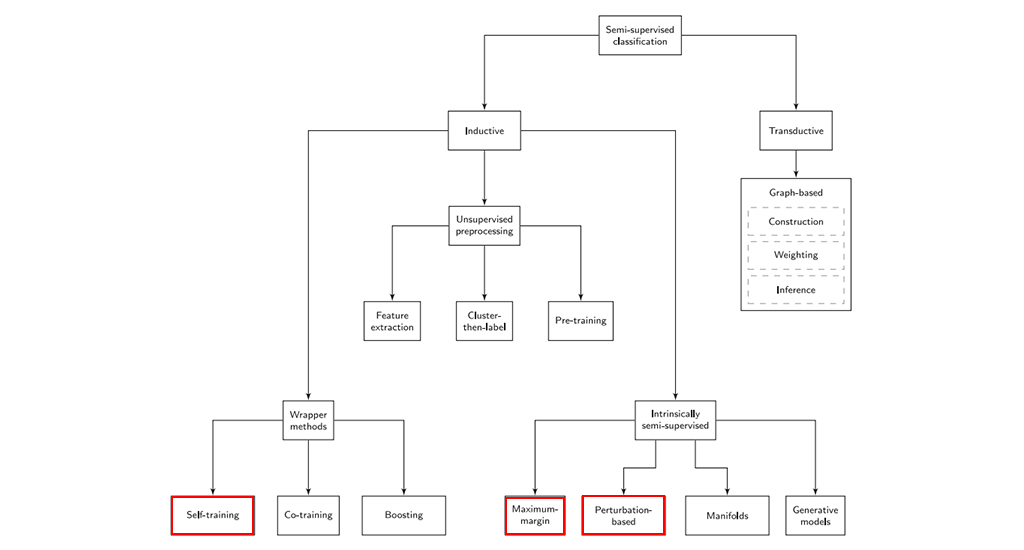
SSL은 분야가 큰 만큼 다양한 종류의 알고리즘이 제안되었습니다. 이러한 알고리즘들은 알고리즘을 기반에 둔 가정, 레이블되지 않은 데이터의 사용 방식, SL과의 연관 관계 등에서 차이를 가집니다. [2]에서는 SSL 방법론들을 inductive / transductive로 나누고, inductive method를 다시 wrapper method, unsupervised preprocessing, intrinsically semi-supervised의 세 종류로 나누었습니다. 그림 4는 [2]에서 나눈 SSL 방법론의 분류 체계를 보여주고 있는데요. 본 포스팅에서는 SSL의 분류 전체를 다루기에는 그 양이 많기 때문에 현재 딥러닝 쪽에서 많이 사용되는 SSL 접근법인 self-training, minimum-margin, perturbation-based에 대한 간략한 설명과 함께 읽어볼 만한 논문을 소개하려고 합니다.

1. Wrapper methods: self training

먼저 wrapper method는 가장 기본적인 SSL 방법입니다. 해당 procedure는 크게 ‘pseudo-labeling’과 ‘학습’ 두 단계로 나뉩니다. 먼저, Pseudo-labeling 단계에서는 모델을 이용해 레이블되지 않은 데이터의 레이블을 예측해서 임시 레이블을 부여합니다. 그리고 학습 단계에서는 레이블된 데이터와 pseudo-label이 붙은 데이터를 합쳐서 일반적인 SL 방식으로 학습을 합니다. 이 방식의 장점은 거의 어떤 SL 모델에도 적용 가능하다는 점입니다. 참고로, [2]에서는 wrapper method를 (1)얼마나 많은 분류기들을 사용하는지, (2)다른 종류의 분류기가 사용되었는지, (3)single-view인지 multi-view인지에 따라 나누었습니다.

wrapper method 중 하나인 Self-training은 그 중에서도 가장 단순한 pseudo-labeling 방법인데요. 하나의 SL 분류기를 사용하여 레이블된 데이터와 이전 반복 단계에서 pseudo-label 된 데이터를 이용해서 계속해서 분류기를 학습합니다. 학습 초기에는 레이블된 데이터만 이용하여 학습하다가 점진적으로 레이블되지 않은 데이터들을 pseudo-labeling 하여 학습에 사용합니다.

2. Intrinsically semi-supervised: maximum-margin, pertubation-based

Intrinsically semi-supervised 방법은 직접적으로 레이블된 데이터와 레이블되지 않은 데이터를 사용하여 목적 함수를 구성하는 접근법입니다. Self-training 방법처럼 중간 단계를 거치거나 base learner를 필요로 하지 않으며, 이미 존재하는 지도학습 방법에 레이블되지 않은 샘플이 포함되도록 목표 함수를 확장합니다. 현재 딥러닝에서 자주 사용되는 방법이며, perturbation-based 방법이 특히 많이 사용되고 있습니다.

여기에는 maximum-margin 방법이 속하는데요. 이 방법 중 하나인 Density regularization는 결정 경계가 확률 밀도가 낮은 곳을 지나가게 하도록 만드는 방식입니다. 이를 위한 방법으로는 예측된 posterior class probability가 overlap 된 정도를 목적 함수에 넣는 방법이 있습니다. [5]에서는 이를 위해 entropy minimization 방법을 제안하였고, 여기서는 conditional entropy를 overlap을 측정하기 위한 지표로 사용하였습니다. 이 방법은 현재도 딥러닝에 포함되어[10] SSL의 성능을 높이는 데에 사용되고 있습니다.

이 밖에도 Perturbation-based 방법이 있는데요. 이 방법은 smoothness 가정에 기반하는데, smoothness 가정은 입력값에 perturbation이 있더라도 모델이 예측한 값이 안정적이어야 한다는 것을 포함합니다. 이는 입력값에 작은 노이즈를 더했을 때, 예측값이 원래 입력값과 비슷해야 한다는 것을 의미합니다. [4]에서는 이 방법을 consistency regularization이라고 부르고 있습니다. 이러한 명칭을 사용한 것은 perturbation-based 방식의 상당수가 원래 입력과 노이즈를 더했을 때의 결과물이 일관되게 예측하도록 하는 정규화 항(regularization term)을 사용하기 때문으로 보입니다. 따라서 여러 방법론들을 보면 어느 정도 비슷함을 느끼실 수 있을 것이라 생각됩니다.

pseudo-ensemble[6]은 모델에 perturbation을 도입한 방법입니다. 이 방법은 기존에 dropout이 여러 모델의 ensemble과 유사하다는 아이디어로부터 dropout을 통해 모델에 perturbation을 주고(child models), 이 모델들의 예측값과 모델 중간의 활성화 값(activations)을 이용하여 목적 함수를 구성합니다.

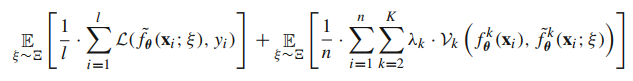
목적 함수의 좌측은 perturbation을 넣은 모델의 예측값을 이용한 loss입니다. 노이즈 $ \xi $를 추출하여 dropout을 적용한 모델의 output과 label 사이의 loss를 구합니다. 이는 다음과 같이 표현됩니다.

우측은 perturbation을 넣은 모델의 활성화 값들이 원래 모델의 활성화 값과 같아지도록 하는 loss입니다. 좌측과 마찬가지로 노이즈를 추출하여 모델에 dropout을 적용하는데, 좌측과의 차이점은 정상적인 입력값의 activation과 dropout이 적용된 activation 값이 같아지도록 한다는 점입니다. 이는 다음과 같습니다.

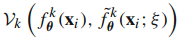
Π-model[7] 역시 전형적인 perturbation 방식 중 하나입니다. Π-model은 하나의 입력값으로부터 data augmentation, network dropout을 이용하여 두 개의 출력값을 만들고, (1)두 값의 차이를 이용한 loss(mse)와 (2)하나의 출력값과 레이블을 이용한 loss(cross-entropy)를 이용하여 학습합니다. 모델의 전체적인 구조는 그림 5와 같습니다.

목적 함수는 다음과 같습니다.

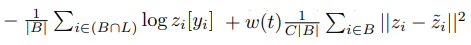
좌측이 예측값을 이용한 loss이며, 우측이 consistency loss(mse)입니다. 좌측은 미니배치 안에서 레이블이 있는 데이터만을 대상으로 하여 계산되며($ i \in ( B \cap L ) $), 우측은 미니배치 전체를 대상으로 계산됩니다($ i \in B $). 위의 pseudo-ensemble 방식과 비교하였을 때 구성이 유사함을 알 수 있습니다.

Virtual adversarial training(VAT)[8]은 perturbation-based 방법 중에서도 어떻게 perturbation을 만드는지에 집중한 방법입니다. 해당 방법은 adversarial example로부터 아이디어를 얻었는데, 간단하게 말하자면 모델이 틀릴 만한 perturbation을 만들자는 것입니다. 기존 perturbation-based 방법들은 perturbation을 만들 때 random하게 만드는 경우가 많았는데 (random noise, model dropout, …) VAT에서는 먼저 noise를 샘플링한 후에, 해당 noise를 더한 값과 기존 값의 차이(KL-div)의 gradient를 이용하여 noise를 생성합니다.

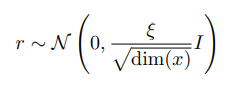
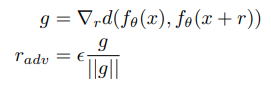
학습은 정상적인 입력값에 대한 예측과 $ r_{adv} $를 이용해 perturbation을 준 입력값 사이의 차이를 목표 함수로 사용하여 진행합니다. 이는 다음과 같습니다.

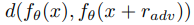
Mixup[9]은 비교적 최근에 나온 방법입니다. 기존 perturbation 방법들은 정상 입력과 perturbation을 넣은 입력값이 동일하도록 했는데, mixup의 아이디어는 perturbation이 결정 경계에서 멀어지는 정도에 비례하여 모델의 출력도 바뀌어야 한다는 것입니다. 이를 위해 mixup에서는 안정적인 모델이라면 특징 벡터의 선형 결합에 대한 예측값이 레이블의 선형 결합이 되어야 한다고 가정합니다. 이를 적용하기 위한 방법 자체는 간단한데, 학습할 때 레이블된 데이터를 둘 랜덤하게 뽑아서 둘을 섞어서 새로운 데이터를 만들고 이를 SL 방식으로 학습에 활용합니다. 학습을 위한 데이터는 데이터 포인트 $ ( x_i, y_i ) $와 $ ( x_j, y_j ) $가 있을 때,

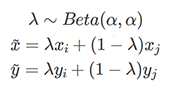
와 같이 만들어집니다. 레이블이 없는 데이터에 대한 mixup은 모델을 이용하여 레이블을 예측한 후에 이를 이용하여 mixup을 진행합니다.

3. Paper 소개: Mixmatch

마지막으로 앞서 언급한 다양한 SSL 방법론을 적용한 논문을 소개하려고 합니다. Mixmatch[10]는 data augmentation + self-training + sharpening(= entropy minimization) + mixup으로 구성된 SSL 방법론입니다. 해당 방법론은 주어진 labeled data batch와 unlabeled data batch로부터 새로운 labeled data batch와 pseudo-labeled data batch를 만들어내며, 이 과정은 다음과 같은 단계로 진행됩니다.

Mixmatch 알고리즘은 우선 주어진 레이블 된 데이터로부터 data augmentation을 통해 새 데이터를 생성하고 (line 3), 그 후에 레이블이 없는 데이터에 대한 data augmentation을 진행하는데, 이때 label이 없는 데이터의 pseudo-label을 K개의 augment 된 데이터에 대한 예측의 평균값에 sharpening을 하여 사용합니다 (line 4-8). 그 후에는 augment 된 데이터들을 섞은 후 레이블 된 데이터들끼리 mixup (line 13), pseudo-label 된 데이터들끼리 mixup (line 14)을 하여 학습에 사용할 데이터를 생성합니다.

여기에서 만들어지는 새로운 데이터들은 실제 레이블과 pseudo-label을 가지고 있으며, 학습은 Intrinsically semi-supervised 방식에서 하는 것처럼 labeled data를 이용한 loss와 pseudo-labeled data를 이용한 consistency loss를 사용하게 됩니다.

loss를 보았을 때, 위에서 언급한 다른 방식들과의 유사성을 찾을 수 있습니다. Mixmatch의 적용 과정을 보았을 때, 기존 방법들과의 차이점은 pseudo-labeling을 하는 방법이 될 것 같습니다. Mixmatch에서는 pseudo-labeling 시에 여러 데이터에 대한 예측을 한 후에 이를 평균하여 여러 augment 된 데이터들에 대한 예측값으로 사용하는데, 이러한 방법이 perturbation에 대해 안정적인 레이블을 제공할 수 있었지 않았나 생각됩니다.

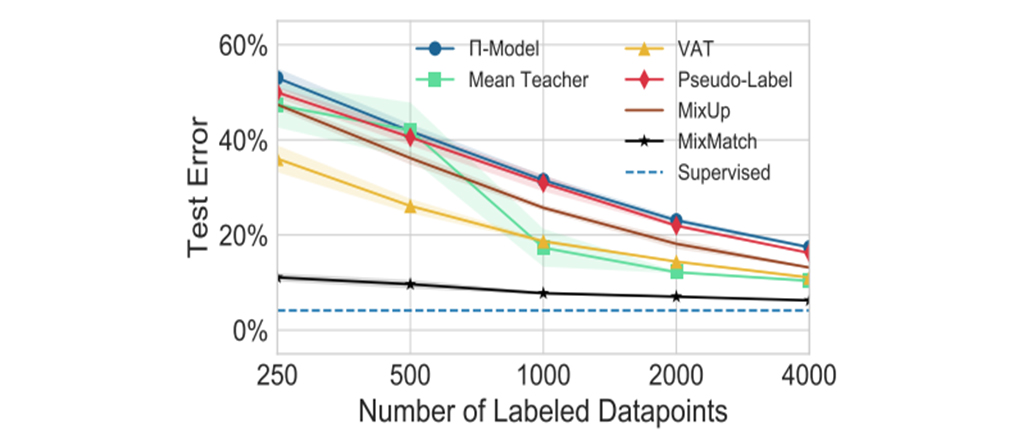
그림 6와 7을 보면 여러가지 SSL 방법들을 함께 쓴 만큼 다른 기법들에 비해 좋은 성능을 보여주고 있습니다.

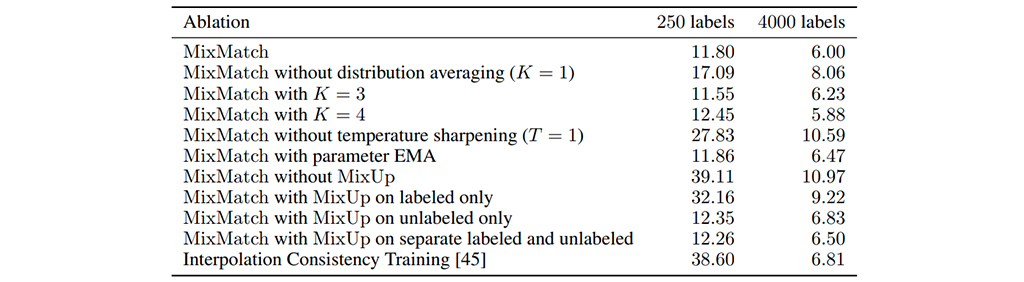
또한, 해당 논문에서 흥미로운 내용이 ablation study인데, 표 1을 보면 mixmatch가 여러가지 SSL 기법들을 섞은 만큼, 각 기법들을 제외하면서 결과가 달라지는 것을 기록하였습니다. 이를 보면 mixup, sharpening, distribution averaging 순으로 효과가 좋을 것으로 예상할 수 있습니다. SSL을 적용하고자 하시는 분들은 참고하시면 도움이 되실 것이라 생각됩니다.

SSL 적용 시 주의점

지금까지 SSL의 장점과 방법론에 대해 이야기했지만, 사실 SSL이 SL 모델의 성능을 반드시 개선해주는 것은 아닙니다. 기존의 연구들로부터 데이터의 가정에 맞지 않은 모델을 사용할 경우, 레이블이 없는 데이터를 추가하여도 성능이 개선되지 않거나 오히려 성능이 떨어지는 경우도 존재합니다 [4]. 그림 8은 SSL의 전형적인 예시 데이터인 ‘two moons’ 데이터셋을 대상으로 앞에서 이야기한 SSL 방법들을 적용했을 때의 결정 경계를 그린 그림입니다. 데이터 분포를 보면 모델의 결정 경계가 곡선으로 만들어져야 바람직한데, Pseudo-label 방법과 Entropy Minimization 방법은 레이블 되지 않은 데이터들을 가로지르는 형태로 결정 경계가 생기는 것을 알 수 있습니다. [4]에서는 Entropy Minimization 방법이 이상한 결정 경계를 만든 것에 대해, 정상적이지 않은 결정 경계 중에서도 confident한 경계가 있을 수 있으며, 뉴럴 네트워크가 output logit의 크기를 늘리는 방식으로 이런 경계에 쉽게 overfit 할 수 있기 때문에 그렇게 된 것 같다는 분석을 하였습니다. 이와 같이 잘 알려진 SSL 방법론들이더라도 항상 기본 모델의 성능을 향상시켜줄 수 있는 것은 아닙니다.

어떤 방법론들이 내 모델에 잘 어울리는지를 사전에 알기는 쉽지 않은데요. [2]에서는 어떤 경우에 모델의 성능 향상을 얻을 수 있는지에 대한 힌트로, 해결하고자 하는 문제의 도메인과 모델의 특성을 고려해 보는 것을 이야기하고 있습니다. 예를 들어 그래프 기반 방법은 각 데이터 포인트 사이의 유사도가 중요하지만, 이미지 같은 경우는 데이터 간의 유클리드 거리가 유사도의 좋은 지표가 되기 어렵습니다. 오히려 이미지에는 입력에 작은 perturbation이 포함되도 안정적인 예측을 하는 특성이 필요한데, 이는 smoothness 가정과 관계되어 있습니다. 또한, 각 지도학습 방법을 확장한 SSL은 기존 모델이 잘 동작하는 상황과 같은 가정을 하기 때문에, 기존 모델이 잘 동작했을 경우 해당 모델의 SSL 확장은 자연스러운 선택이 될 수 있습니다. 이와 같이 실제 SSL 방법론의 적용에는 모델, 데이터, 방법론들의 특징을 잘 고려하여 적절한 방법을 찾아야 좋은 효과를 얻을 수 있을 것입니다.

Conclusion

지금까지 SSL의 기본적인 지식과 방법론들, 딥러닝에서의 활용 등에 대해 알아보았습니다. 현재 딥러닝을 적용하고자 하는 여러 회사들에서 가장 많은 비용을 지불하고 있는 분야가 바로 서비스에 맞는 데이터셋 확보인 만큼, 데이터셋 확보에 상당한 비용이 소요되고 있는데요. 상대적으로 적은 비용과 노력으로 수집 가능한 unlabeled dataset을 활용하여 모델의 성능을 높일 수 있다는 점은 바로 SSL의 가장 큰 매력이라고 생각합니다.

또한, 최근 딥러닝 연구에서 학습 모델과 기법의 공개가 활발하게 이루어지고 있는 추세이기 때문에 그 외적인 부분에서 차이를 둔다면 큰 경쟁력이 될 것입니다. 사실상 적은 레이블 데이터를 가지고 모델을 훈련시킬 수 있다는 것은 많은 ML 연구자들이 꿈꾸는 것 중 하나라고 생각하는데요. 연구자 입장에서 본다면, SSL 연구가 오래된 만큼 그 안에서 사용된 기존 방법론들을 딥러닝에 새롭게 적용시켜보는 것도 좋은 연구 주제가 될 것 같습니다. 다만, 앞선 연구들에서 언급하였듯이 SSL이 무조건적인 성능의 향상을 보장하는 것은 아니며, 널리 사용하는 방법들도 이상 동작을 보일 수 있습니다. 본인의 모델에 잘 맞는 SSL 기법을 적용하기 위해 다양한 고민과 선택을 하는 과정 속에서 이 포스팅이 좋은 길잡이가 되기를 희망합니다.

참고문헌

[1] https://www.kdnuggets.com/2019/11/tips-class-imbalance-missing-labels.html
[2] Van Engelen, Jesper E., and Holger H. Hoos. “A survey on semi-supervised learning.” Machine Learning 109.2 (2020): 373-440.
[3] Chapelle, Olivier, Bernhard Schlkopf, and Alexander Zien. “Semi-Supervised Learning.” (2010).
[4] Oliver, Avital, et al. “Realistic evaluation of deep semi-supervised learning algorithms.” Advances in neural information processing systems. 2018.
[5] Grandvalet, Yves, and Yoshua Bengio. “Semi-supervised learning by entropy minimization.” Advances in neural information processing systems. 2005.
[6] Bachman, Philip, Ouais Alsharif, and Doina Precup. “Learning with pseudo-ensembles.” Advances in neural information processing systems. 2014.
[7] Laine, Samuli, and Timo Aila. “Temporal ensembling for semi-supervised learning.” arXiv preprint arXiv:1610.02242 (2016).
[8] Miyato, Takeru, et al. “Virtual adversarial training: a regularization method for supervised and semi-supervised learning.” IEEE transactions on pattern analysis and machine intelligence 41.8 (2018): 1979-1993.
[9] Zhang, Hongyi, et al. “mixup: Beyond empirical risk minimization.” arXiv preprint arXiv:1710.09412 (2017).
[10] Berthelot, David, et al. “Mixmatch: A holistic approach to semi-supervised learning.” Advances in Neural Information Processing Systems. 2019.

[ 관련 포스팅 보러가기 ]
AI 앱 개발을 위한 학습용 데이터 구축기 >>>
'디지털 뉴딜' 총 100억 규모 AI 정부사업 수주 소식 >>>