안녕하세요, AI PLUS Tech Blog입니다.
오늘은 생성 모델에 새로 등장하여 뛰어난 성능으로 현재 많은 주목을 받고 있는 확산(diffusion) 모델에 대해 이야기하려고 합니다.
확산 모델은 최근에 새롭게 등장한 생성 모델(generative model)의 일종으로, 기존의 생성 모델에 비해 더 우수한 성능과 유용한 특성들로 인해 많은 관심을 받고 있는 모델입니다. 하지만 확산 모델은 물리학에서 아이디어를 가져와 다소 복잡한 수식이 등장하는 등 기존의 생성 모델들과 비교했을 때, 다소 생소한 부분들이 있는 만큼 확산 모델 등장의 흐름을 따라가며 개념을 정리하는 시간을 가져볼까 합니다.
해당 개념을 다루는 순서는
- 확산 모델에 대한 소개와 점수 함수(score-function)
- 기반 모델에 대한 소개
- 둘을 결합한 SDE를 이용한 점수 기반 생성 모델(score-based generative modeling through SDEs)의 순서로 살펴보도록 하겠습니다.
(본문에 삽입된 이미지는 인용 시 해상도 등의 문제로 원 논문의 내용에 변화가 없는 한에서 새로 작성하였습니다)
생성 모델(Generative Models)
기계 학습 모델은 모델이 하는 일에 따라 크게 분류 모델과 생성 모델로 나눌 수 있습니다. 분류 모델은 일반적으로 고차원의 입력 데이터를 낮은 차원의 레이블 데이터로 변환하는 작업을 합니다.
반대로 생성 모델은 상대적으로 낮은 차원의 데이터로부터 높은 차원의 데이터를 만들어내는 작업을 합니다 (e.g. 개/고양이 레이블 -> 사진, 텍스트 -> 음성).
딥러닝의 대표적인 생성 모델로는 Variational autoencoderVAE, GAN[4]과 최근에 주목을 받은 모델 flow 기반 모델이 있습니다. VAE는 오토 인코더의 파생형으로, 인코더를 통해 입력 값을 특정 확률 분포 상의 한 점으로 만들고, 디코더를 통해 해당 점으로부터 입력 값을 생성해냅니다. VAE는 명시적인 확률 분포를 모델링 한다는 장점이 있으나, 가능도(likelihood)가 아닌 ELBO를 통한 학습이라는 점에서 다소 아쉬움이 존재합니다. 또한 다른 모델들에 비해 비교적 생성된 결과물의 품질이 떨어진다는 단점이 있습니다.
GAN은 위조지폐범과 경찰의 예시로 잘 알려져 있는데, 데이터를 생성하는 생성자(generator), 그리고 주어진 데이터가 실제 데이터인지 생성된 데이터인지를 판별하는 판별자(discriminator)를 동시에 학습시키는 방식입니다. 학습 후에는 생성자를 이용하여 원하는 값을 만들게 됩니다. GAN은 묵시적(implicit)으로 확률 분포를 모델링 하기 때문에 모델 구성에 제한이 없으며 생성된 결과물의 품질이 뛰어난 편입니다. 다만 생성자와 판별자가 같이 학습이 되어야 한다는 점, 모드 붕괴 등 학습에 어려움이 있는 것으로 알려져 있습니다.
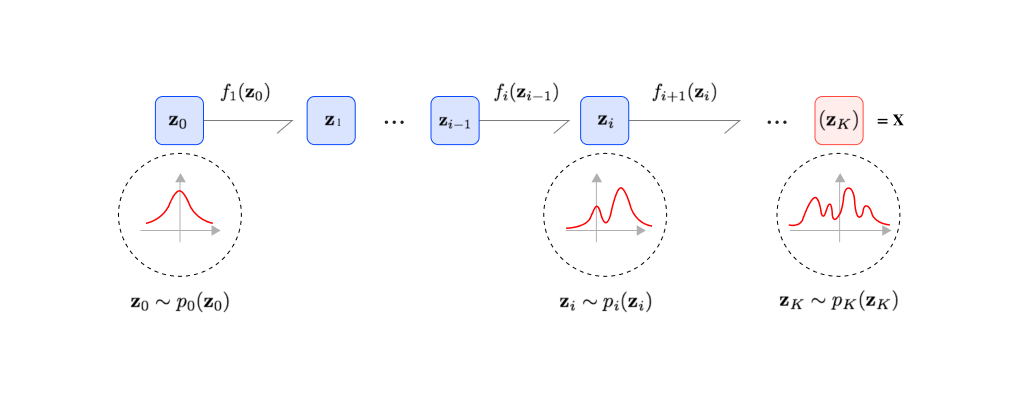
Flow 기반 모델들은 위 두 모델과 또 다른 접근법을 취하는데, 단순한 확률 분포에서 추출된 값에 여러 단계의 변환을 거쳐 복잡한 분포를 만드는 방법입니다 (e.g. 노이즈 데이터 -> 개/고양이 사진). 변환 함수를 파라미터화하여 딥러닝 모델로 학습하는 해당 방법은 명시적으로 정확한 likelihood를 모델링한다는 장점이 있고[9] 생성된 결과물의 품질이 좋습니다. 하지만 변환 함수에 역함수가 존재해야 한다는 제한이 있기 때문에 모델을 만들 때 사용하는 연산자에 제한이 있습니다.
확산 확률 모델(Diffusion probabilistic models)
앞의 생성 모델들이 하는 일은 간략화해서 노이즈와 실제 사진과의 관계를 나타내는 것입니다. VAE는 인코더와 디코더를 통해 사진 -> 잠재 변수 -> 사진에서 잠재 변수를 정규 분포로 만드는 방법을 학습하였고, GAN은 정규 분포 -> 사진의 디코더를 학습한 것입니다. Flow 기반 모델은 이를 여러 단계의 가역함수로 나눈 것입니다.
그렇다면 확산 모델은 어떨까요? 확산 모델은 flow 기반 모델과 비슷합니다. 확산 모델은 초기 상태의 분자들이 시간이 흐름에 따라 흩어지는 것을 나타내는 랑주뱅 동역학(Langevin dynamics)에서 아이디어를 가져왔습니다. 간단히 말하자면, 특정 사진의 픽셀들이 시간이 지나면서 흩어져서 노이즈로 변하는 것을 수식을 통해 나타낸 것입니다.
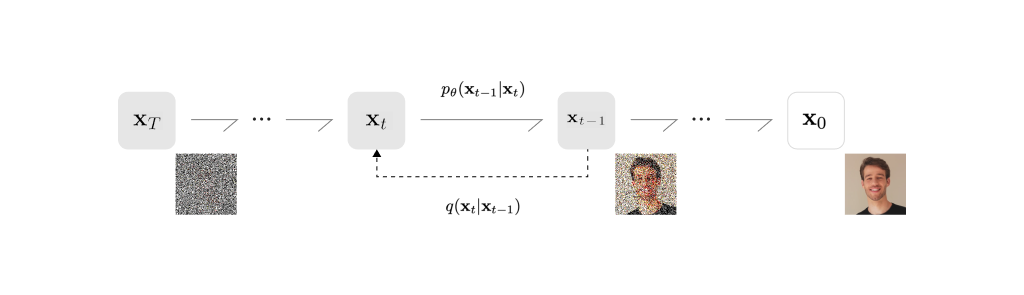
이 변환은 정방향 변환(forward)과 역방향 변환(reverse)으로 나뉩니다. 정상 변환은 데이터가 노이즈로 변하는 것이며, 역변환은 노이즈로부터 데이터가 만들어지는 것입니다.
확산 모델에서는 역변환 단계를 파라미터화 하여 딥러닝 모델로 학습하고, 학습된 역변환을 통해 노이즈로부터 데이터를 생성합니다. 따라서 확산 모델은 유한한 시간 후에 사진을 생성하도록 학습된 파라미터화 된 마르코프 연쇄(Markov chain)라고 할 수 있습니다[7]. 또한 확산 확률 모델에서는 학습에 negative log-likelihood의 ELBO를 사용합니다.
실제 계산을 위해서는 $ p $와 $ q $의 분포를 정할 필요가 있으며, [5]에서는 정규분포와 이항분포에 대한 정방향 변환, 역방향 변환을 제시하였습니다.
점수 기반 생성 모델(Score-based generative models)
Score-based generative modeling through SDEs를 알기 위해 봐야 할 다른 한 갈래는 점수 기반 생성 모델Score-based generative models입니다.
점수 기반 생성 모델의 핵심 아이디어는 바로 랑주뱅 동역학을 이용하여 샘플을 생성할 때 점수 함수(score function)을 이용한다는 것과 점수 함수를 사전에 실제 데이터로부터 학습해둔다는 것입니다. 해당 모델에서 이미지 생성 시의 수식은 다음과 같습니다.
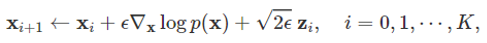
여기서 $ mathbf{x}_0 $는 일반적으로 샘플링 된 노이즈이고, 여기에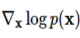
를 통한 업데이트를 반복적으로 적용하여 원하는 이미지를 얻습니다 이 때, 
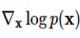가 바로 점수 함수입니다.
하지만 점수 함수의 
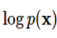값은 실제 데이터의 확률 분포이기 때문에 알 수 없습니다. 점수 기반 생성 모델에서는 이 문제를 해결하기 위해 파라미터화 한 뉴럴 네트워크를 통해 점수 함수를 학습하는 방식을 사용하였습니다.
따라서 다음과 같은 함수를 정의하고,
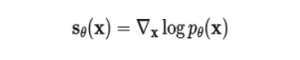
다음과 같은 loss를 통해 실제 데이터로부터 점수 함수를 학습하게 됩니다. 이렇게 할 경우 기존 [5,7]처럼 미리 정해둔 분포가 아니라 보다 복잡한 분포를 사용할 수 있다는 장점이 있습니다.
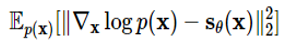
따라서 전체적인 점수 기반 생성 모델의 흐름은
- 실제 데이터로부터 점수 함수 학습,
- 랑주뱅 동역학을 이용한 이미지 생성으로 이루어지며, 이를 그림으로 구현하면 다음과 같습니다.
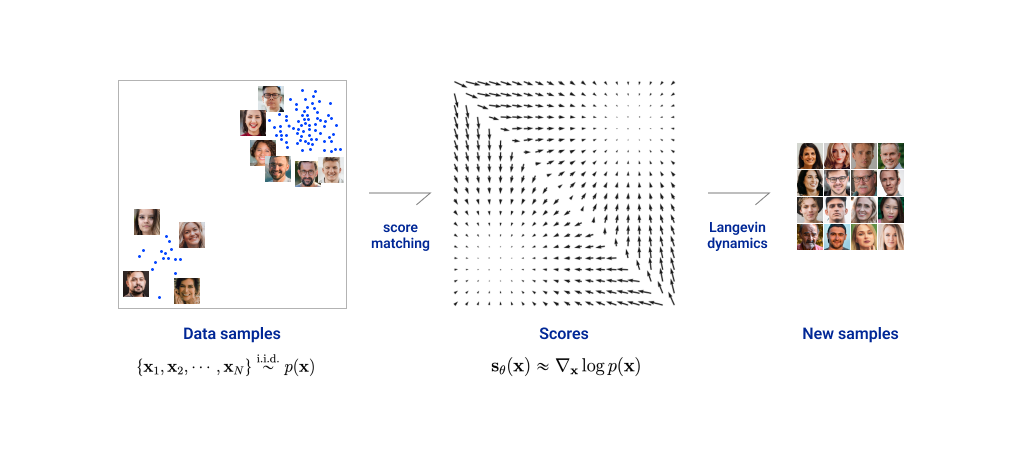
다만 점수 함수를 학습하게 되면서 이에 따른 추가적인 문제점들이 발생하는데, 바로 데이터 공간에서 데이터가 적은 지역들에 대한 예측 값이 정확하지 않다는 점입니다.
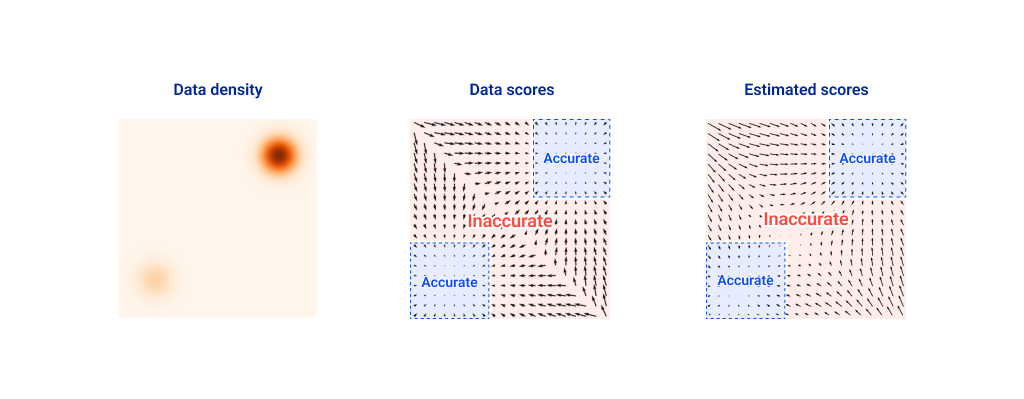
이런 문제점을 해결하기 위해서 [6]에서는 다음과 같이 실제 데이터 분포에 여러 스케일의 가우시안 노이즈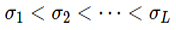
를 섞은 분포를 정의하였습니다.
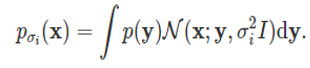
그리고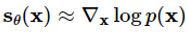
로 노이즈가 섞인 데이터 분포의 점수 함수를 학습하는 뉴럴 네트워크를 정의하고, 다음과 같은 loss를 통해 해당 네트워크를 학습하도록 하였습니다.
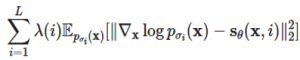
위와 같은 방법을 통해 데이터가 적은 지역에서의 예측 정확도를 높이고 생성되는 샘플의 품질을 높였습니다.
Score-based generative modeling with stochastic differential equations (SDEs)
Score-based generative modeling with stochastic differential equations[8]에서는 위의 점수 함수에 노이즈를 더하는 방법에서 노이즈의 단계를 무한대로 확장하여 연속적으로 다룰 수 있게 하였습니다. 점수 기반 생성 모델의 이미지 생성은 시간에 대한 stochastic process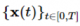 
로 볼 수 있습니다. 해당 프로세스는 다음과 같은 stochastic differential equation의 해로 얻어집니다.
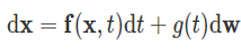
해당 방정식에서 w는 위너 프로세스로, 주어진 시간 t에 대한 노이즈 텀이라고 볼 수 있습니다. 여기서 g(t)를 구성하는 방식에 따라 위에서 말한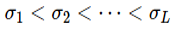 
와 같이 시간에 따라 점차 커지는 노이즈를 만들어 줄 수 있습니다. 따라서 위 SDE의 해로 얻어지는 stochastic process는 위의 노이즈 데이터 분포 를 따른다고 할 수 있습니다.
그리고 더 중요한 것은 위 방정식의 역방향 방정식입니다. 앞에서 확산 모델의 정방향/역방향 변환과 마찬가지로 SDE에는 역방향이 존재합니다. 역방향 SDE는 다음과 같고, 앞의 확산 모델 때와 마찬가지로 역방향 SDE를 통해 노이즈로부터 샘플을 생성할 수 있습니다.
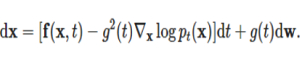
여기서 중요한 것이 바로 
입니다. 역방향 SDE를 계산하기 위해서는 주어진 시간에 대한 점수 함수를 계산할 수 있어야 합니다.
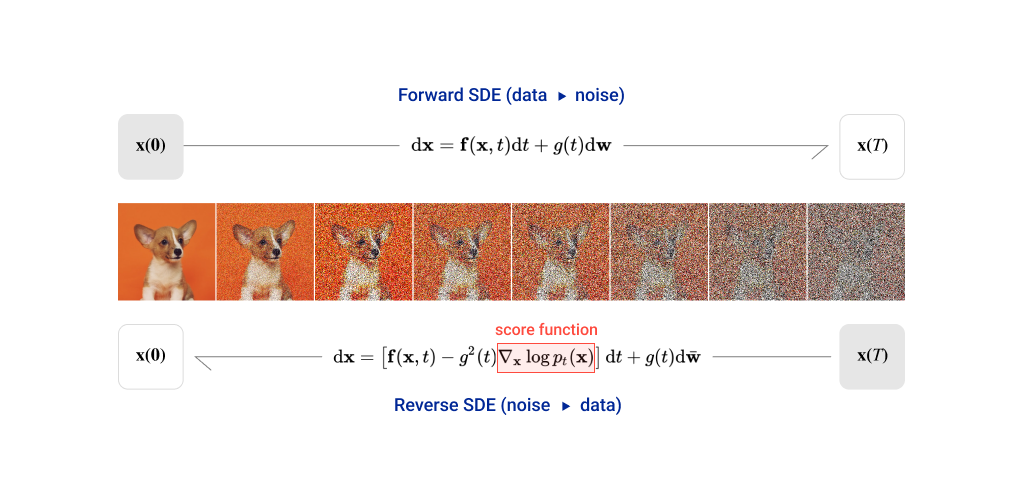
그럼 점수 함수는 어떻게 구해야 할까요?
SDE를 이용한 점수 함수 기반 생성 모델이 기존 점수 함수 기반 생성 모델을 확장한 형태인 만큼, 점수 함수를 얻는 방법도 기존 모델과 비슷합니다. 마찬가지로 데이터의 분포를 학습하기 위한 뉴럴 네트워크를 정의한 후, 데이터 분포와의 L2 loss를 통해 점수 함수를 학습하고, 학습한 값을 역방향 SDE 계산에 사용하는 방식을 사용합니다. Loss는 다음과 같습니다.
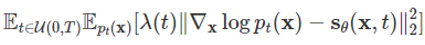
기존 loss와 차이점으로는 앞에 weight term이 들어간다는 것입니다. 해당 term은 다음과 같은값을 사용하였는데,
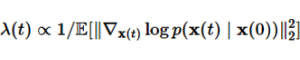
이 값은 여러 t 값들에 대한 loss의 크기를 맞춰주는 역할을 합니다.
이렇게 점수 함수를 학습한 후에는 역방향 SDE를 풀어야 하는데, Euler–Maruyama법과 같은 SDE를 푸는 일반적인 방법을 사용하여도 되지만, [8]에서는 Predictor-Corrector 샘플러 라는 방법을 사용하였습니다.
Predictor-Corrector 샘플러 방식은 이름 그대로 이미지를 생성할 때 predictor와 corrector의 쌍을 사용하는 방식입니다. Predictor는 매 시간(time step)마다 역방향 SDE를 계산하여 먼저 샘플을 생성하고(prediction), corrector는 해당 이미지를 점수 함수를 사용하여 수정(score-based MCMC)합니다. 논문에서 제시한 predictor/corrector는 다음과 같으며, predictor의 수식은 점수 함수가 학습하는 노이즈 데이터 분포를 어떻게 구성하느냐에 따라 조금씩 달라집니다. 다음 알고리즘들은 서로 다른 predictor를 사용한 PC 샘플러 알고리즘을 보여줍니다.
[8]의 CIFAR-10을 이용한 실험에서는 전반적으로 VP SDE 방식이 더 좋은 성능을 보여주었습니다.
Probability flow ODE
Probability flow ODE는 위의 SDE를 ODE(ordinary differential equations)로 변형한 것입니다. 이때 ODE에서 얻어지는 분포()는 원래의 SDE와 같습니다. 수식은 다음과 같으며, 기존 SDE의 노이즈 항이 없어진 것을 알 수 있습니다.
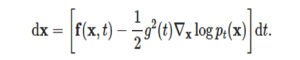
이렇게 만들어진 probability flow ODE는 normalizing flow의 일종이기도 하기 때문에 정확한(exact) log-likelihood를 계산할 수 있고, 또한 invertible한 성질도 가지고 있습니다.
맺는 말: Diffusion model in TTS
지금까지 확산 모델의 등장과 그 발전에 대해 알아보았습니다. 이런 모델은 한번 나오면 다양한 분야에 접목될 수 있습니다.
실제 확산 모델의 논문은 컴퓨터 비전(vision) 분야의 논문에 등장하였지만, 현재는 TTS 등 다른 분야에서도 많은 관심을 가지고 다양하게 사용되고 있습니다.
이스트소프트가 올해 10월에 개최했던 AI PLUS 2021에서 선보인 AI 아나운서의 음성 생성에도 해당 확산 모델이 사용되었습니다.
과연 앞으로는 또 어떤 새로운 모델들이 더 진짜 같은 이미지와 음성을 만들어내는데 사용될까요? 이 글이 새로 등장한 확산 모델에 관심 있는 분들의 이해와 지식 확장에 조금이라도 도움이 되기를 기대합니다.
감사합니다.
참고문헌
[1] https://lilianweng.github.io/lil-log/2021/07/11/diffusion-models.html?fbclid=IwAR00YkyNYkNvP3ObObi02aqY95Tl-huSqfV7g2ZC1BfK7aJDTzvmEA4EBiw
[2] https://yang-song.github.io/blog/2021/score/
[3] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).
[4] Goodfellow, Ian, et al. “Generative adversarial networks.” Communications of the ACM 63.11 (2020): 139-144.
[5] https://arxiv.org/pdf/1503.03585.pdf
[6] Yang Song & Stefano Ermon. “Generative modeling by estimating gradients of the data distribution.” NeurIPS 2019.
[7] Jonathan Ho et al. “Denoising diffusion probabilistic models.” arxiv Preprint arxiv:2006.11239 (2020).
[8] Yang Song et al. “Score-Based Generative Modeling through Stochastic Differential Equations.” ICLR 2021
[9] Kingma, Diederik P., and Prafulla Dhariwal. “Glow: Generative flow with invertible 1x1 convolutions.” arXiv preprint arXiv:1807.03039 (2018).