이번 포스팅에서는 이스트소프트 A.I. PLUS Lab이 ICLR 2020에서 발표한 “Regularizing activations in neural networks via distribution matching with the Wasserstein metric” 연구를 소개하겠습니다.

본 연구는 Wasserstein 확률공간에서 네트워크를 regularization하는 방법을 제시하였습니다. 이 방법론을 자세하게 소개하기 전에 기존에 주로 활용되던 통계 기반 방법론들의 문제점을 간단히 살펴보겠습니다.

통계 기반의 regularization/normalization 방법론의 한계

뉴럴 네트워크의 학습을 안정화시키고 generalization 성능을 향상시키기 위하여, activation 값을 regularization/normalization하는 방법들은 다양한 모델의 building block으로 자리잡았습니다.

가장 대표적으로 사용되는 batch normalization (BN; Ioffe & Szegedy, 2015)은 activation값들의 평균과 분산을 표준화한 뒤, 추가 파라미터 $\gamma$와 $\beta$를 도입하여 scale과 shift연산을 적용합니다. 즉, activation 값들이 $\{ h_i \}_{i=1}^{n}$일 때, $h_i$ 의 값은 다음과 같이 표현됩니다. $ BN(h_i; \{ h_i \}) = \gamma \left( \frac{h_i - \mu(\{ h_i \})}{\sigma(\{ h_i \})+\epsilon} \right) + \beta $ 위 식에서 $\mu(\{ h_i \})$와 $\sigma(\{ h_i \})$는 $\{ h_i \}$의 평균과 표준 편차를 뜻하며, $\epsilon$는 numerical stability를 위한 작은 상수(예: $10^{-8}$)입니다.

또한, BN이 개별 유닛의 관계를 고려하지 못하는 한계를 극복하기 위하여, decorrelated BN (DBN; Huang et al., 2018)은 whitening operation을 사용하였습니다. 이 외에도, 표본 분산의 분산을 최소화하여 4차 모멘트를 최소화하는 variance consistency loss (VCL; Littwin & Wolf, 2018)방법이 있습니다. 흥미롭게도, 4차 모멘트를 최소화하는 것은 adaptive mode separation을 가능하게 합니다.

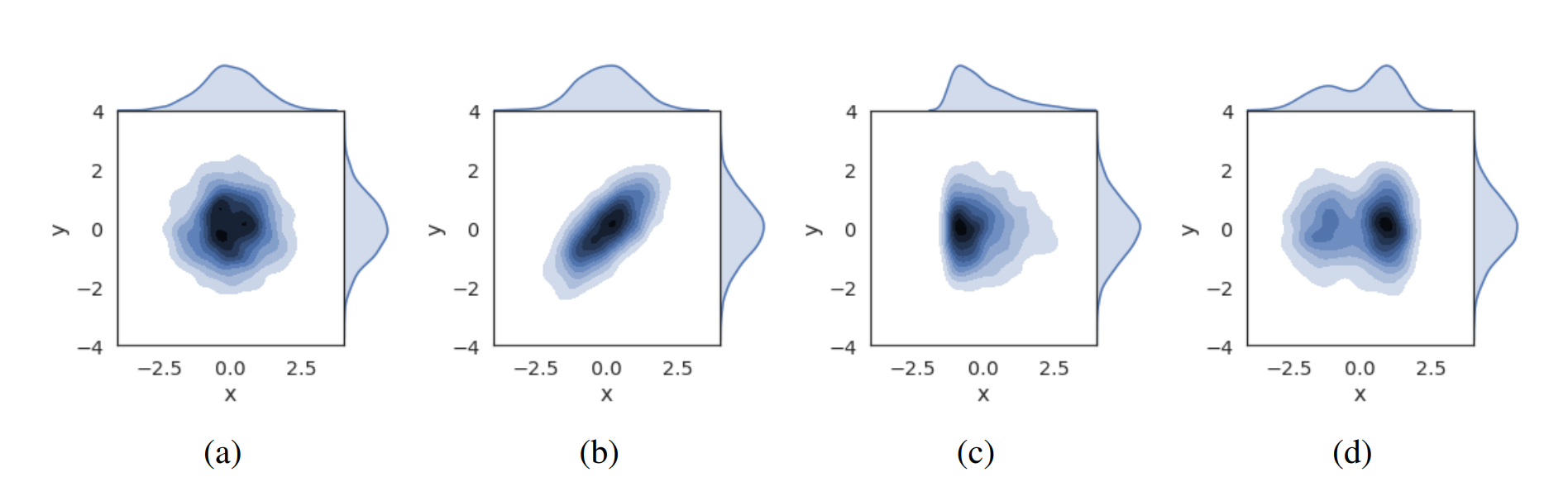
위 방법들은 activation 값들의 통계값을 기반으로 동작합니다. 통계량은 확률분포에서 중요한 정보를 간단하고 효과적으로 추출하지만, 미리 정의되지 않은 확률분포의 특성을 고려하지 못하는 단점이 있습니다. 예를 들어, 그림 1의 모든 경우에서 x는 평균 0 분산 1을 갖지만, 각각의 경우들은 correlation, skewness, multi-modality와 같은 다양한 특성을 갖습니다. 이때, 만약 확률 변수 x를 표준 정규분포 확률변수 y가 되도록 regularization/normalization하는 경우 표준화 기반의 방법론(BN)은 모든 경우를 동일하게 취급하고, whitening 기반의 방법론(DBN) 은 a,c,d를 동일하게 취급합니다.

Projected error function regularization 제안

저희는 통계량을 이용하는 기존 방법의 한계에 motivate되어, 확률공간에 정의된 거리를 이용하는 아이디어를 바탕으로 projected error function regularization (PER)을 제안하였습니다. PER는 정규분포와 미니배치 activation값들로 이루어진 empirical 분포의 Wasserstein 거리를 최소화하는 방법론입니다. 이때, 효율적인 연산을 위하여 Wasserstein 거리와 equivalent한 sliced Wasserstein 거리를 이용하였으며, 이는 다음과 같이 표현할 수 있습니다.

$ SW_1 (\mu,\nu) = \int_{\mathbb{S}^{d-1}} W_1(\mu_\theta,\nu_\theta) d \lambda(\theta) \\ = \int_{\mathbb{S}^{d-1}} \int_{- \infty}^{\infty} \left| F_{\mu_\theta}(x) - \frac{1}{b} \sum_{i=1}^{b} 1_{\langle h_i, \theta \rangle \leq x} \right| dx d \lambda(\theta) $

위 식에서 $\mu$는 Gaussian measure이고, $\nu$는 activation 값들의 집합($\{ h_i \}$)으로 이루어진 empirical 분포의 measure입니다. 또한 $\mu_\theta$와 $\nu_\theta$는 각 measure를 각도 $\theta$로 투영시킨 1차원 실수 위에 정의되는 measure입니다.

하지만, 위 식을 계산하기 위해서 activation 값들의 정렬 연산이 필요합니다. 샘플 간 연산 상의 의존 관계가 발생함에 따라, 병렬 학습을 할 때 문제가 됩니다. 또한, 정렬 연산의 비용은 배치 크기가 커지게 되면 무시할 수 없게 됩니다. 따라서, 위 식에 Minkowski inequality를 적용하여 최종 regularization loss를 구하였습니다.

$ SW_1 (\mu,\nu) \leq \int_{\mathbb{S}^{d-1}} \int_{- \infty}^{\infty} \frac{1}{b} \sum_{i=1}^{b} \left| F_{\mu_\theta}(x) - 1_{\langle h_i, \theta \rangle \leq x} \right| dx d \lambda(\theta) \\ = {\frac{1}{b}} \sum_{i}^{} \int_{\mathbb{S}^{d-1}} \left( \langle h_i, \theta \rangle \text{erf}\left(\frac{\langle h_i, \theta \rangle}{\sqrt{2}}\right) + \sqrt{\frac{2}{\pi}} \exp\left(-\frac{\langle h_i, \theta \rangle^2}{2}\right)
\right) d \lambda(\theta) = \mathcal{L}_{per} (\nu) $

$\mathcal{L}_{per} (\nu)$의 gradient는 다음과 같은 간단한 형태로 나타납니다.

$ \nabla_{h_i}\mathcal{L}_{per} (\nu) = \frac{1}{b} \mathbb{E}_{\theta \sim U(\mathbb{S}^{d_l - 1})} \left[ \text{erf} \left( \langle\theta, h_i / \sqrt{2} \rangle \right) \theta \right] $

네트워크를 학습할 때 $\mathcal{L}_{per} (\nu)$를 계산할 필요가 없기 때문에, 실제 구현에서는 forward pass에서 activation 값들을 cache만 해준 뒤 backward pass에서 gradient만 계산하여 regularization을 적용합니다. 구체적인 구현법은 알고리즘 1과 같습니다.

실험 결과

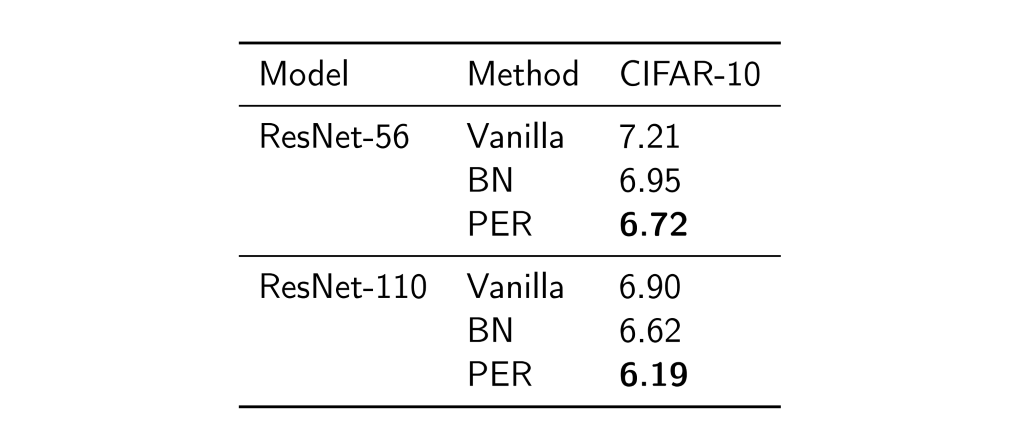
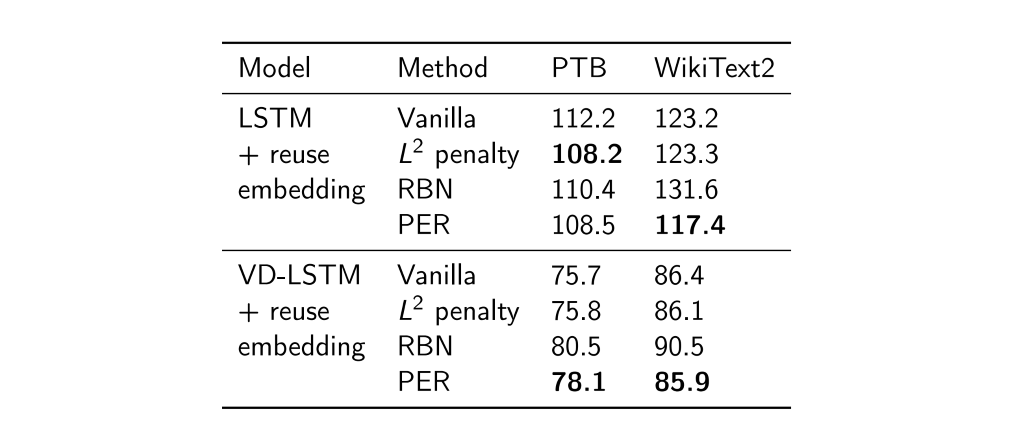
저희가 제안한 PER를 적용했을 때, 벤치마크 결과는 표1, 표2, 표3과 같습니다. 결과를 해석해보면 regularization/normalization 방법을 적용하지 않은 vanilla 모델에 비해 일관된 향상을 보여줍니다. 또한 통계량 기반의 방법론(BN, VCL, recurrent BN (Cooijmans et al., 2017) ) 등과 비교하여 대부분의 경우 성능이 향상된 것을 확인하였습니다.

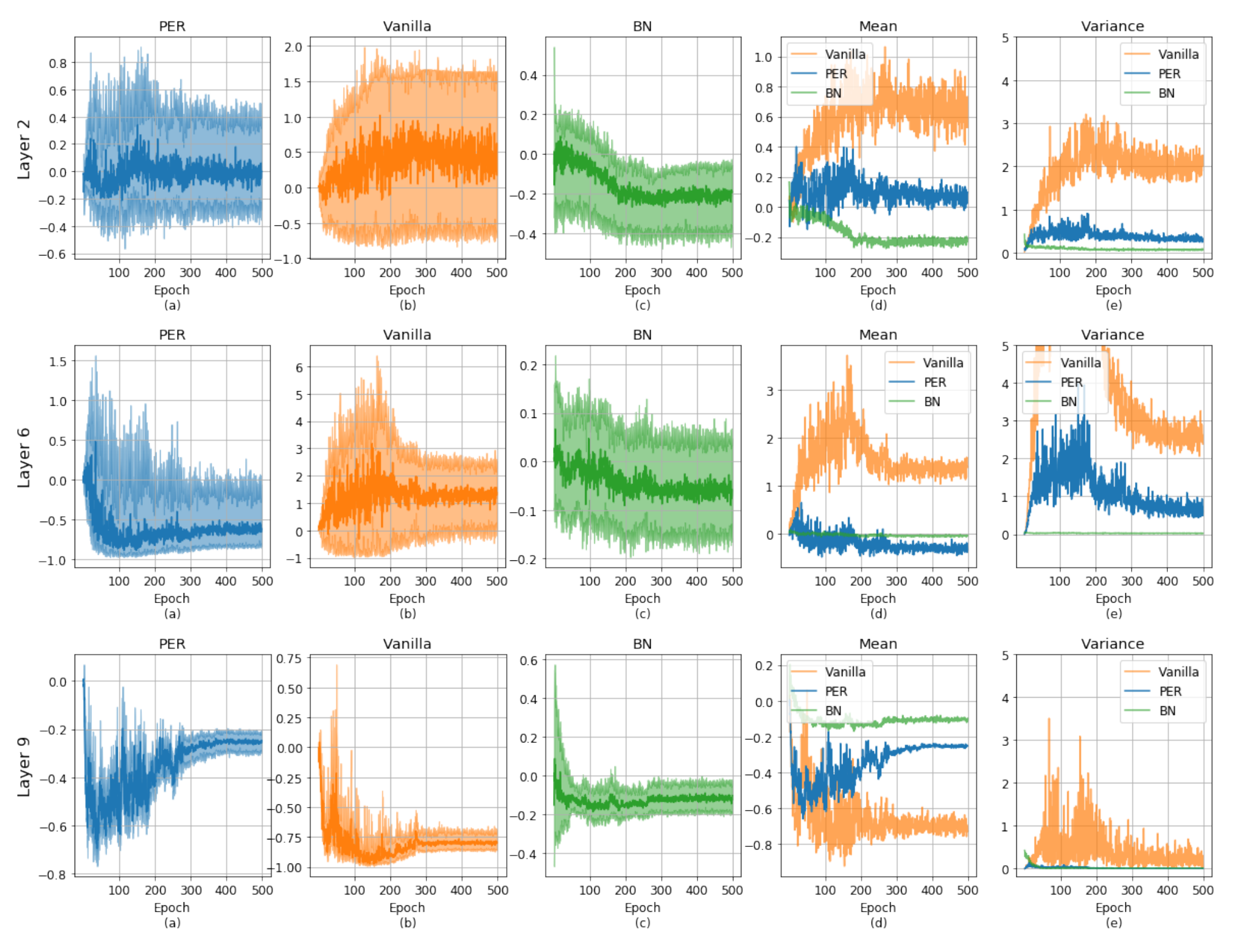
마지막으로, PER가 실제 activation 분포에 어떤 영향을 미쳤는지를 분석하였습니다. 그림 2의 a-c는 PER,vanilla,BN 모델들의 특정 activation 값의 분포를 나타냅니다. BN b의 경우 activation의 $L^2$ norm을 bound하기 때문에 연결된 두 epoch 사이에서 변화 매우 안정적인 것을 확인할 수 있습니다. 반면, vanilla와 PER는 normalization 과정이 없기 때문에 BN에 비해 불안정합니다. 하지만, PER를 이용할 경우 variation가 매우 커지는 현상을 효과적으로 막을 수 있습니다. 구체적으로 그림 2의 d와 e에서 볼 수 있듯이 PER는 초기에 불안정하지만, skew된 평균과 분산을 학습 과정에서 점차 복구됩니다.

Conclusion

지금까지 ICLR 2020에 발표한 “Regularizing activations in neural networks via distribution matching with the Wasserstein metric”를 살펴보았습니다. 오늘 소개드린 연구 외에도, 이스트소프트 A.I. PLUS Lab 에서는 다양한 연구를 진행하고 있으니 많은 관심과 응원 부탁드립니다. 감사합니다.

참고문헌

[1] Djork-Arné Clevert, Thomas Unterthiner, and Sepp Hochreiter. Fast and accurate deep network learning by exponential linear units (ELUs). In ICLR’2016.
[2] Tim Cooijmans, Nicolas Ballas, César Laurent, Çağlar Gülçehre, and Aaron Courville. Recurrent batch normalization. In ICLR’2017.
[3] Yarin Gal and Zoubin Ghahramani. A theoretically grounded application of dropout in recurrent neural networks. In NIPS’2016.
[4] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR’2016.
[5] Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural Computation, 9(8): 1735-1780, 1997.
[6] Lei Huang, Dawei Yang, Bo Lang, and Jia Deng. Decorrelated batch normalization. In CVPR’2018.
[7] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML’2015.
[8] Etai Littwin and Lior Wolf. Regularizing by the variance of the activations’ sample-variances. In NeurIPS’2018.