AI는 인공신경망의 등장부터 두 번의 AI 겨울이 지난 현재까지 많은 산업의 패러다임을 바꿔나가고 있습니다. 특히 금융시장에서는 AI의 잠재력을 높게 평가하고, 현재 시장 트렌드 분석, 미래 시장 변화 예측 등을 위한 최적의 예측 모델을 연구하고 있는데요.

이같은 모델 개발을 위해서는 먼저 ‘초매개변수(하이퍼 파라미터, hyperparameter)’를 설정해야 합니다. 많은 연구들을 통해 알 수 있듯이, 우리는 그동안 경험적으로 최적의 hyperparameter를 찾아 왔습니다. AI 알고리즘의 성능은 각 모델에 최적화된 hyperparameter 구성에 따라 크게 달라지기 때문에, 이때 파라미터 값을 조정하는 것은 매우 중요한 역할을 하는데요.

이번 article에서는 최소 시간과 컴퓨팅 자원을 사용해 최적의 hyperparameter를 찾는 ‘hyperparameter optimization’ 방법론을 살펴보고, 이중 ‘베이지안 최적화(bayesian optimization)’를 알고리즘 트레이딩에서 어떻게 활용할 수 있는지 중점적으로 알아보겠습니다.

What is Hyperparameter Optimization?

Optimization이란 어떤 임의의 함수 f(x)의 값을 최대화 또는 최소화하는 해를 구하는 것입니다. 이 f(x)를 딥러닝 모델이라고 가정하면, 이 모델이 가질 수 있는 layer 개수, dropout 비율, 학습률(learning rate) 등 hyperparameter를 조절하여 성능을 최적화시키는 것을 ‘초매개변수 조정(hyperparameter tuning)’이라고 합니다.

최신 머신러닝 프로세스를 자동화하는 ‘Auto ML’에서는 여러가지 hyperparameter tuning 기법들이 활용되고 있는데요. 최적의 퍼포먼스를 내기 위한 hyperparameter 탐색 기법들은 지속적으로 연구되고 있고, 대표적으로 다음의 4가지가 있습니다.

1) Manual search

Manual search란 사용자가 뽑은 조합 내에서 최적의 조합을 찾는 것을 의미합니다. 아무래도 사용자의 경험이나 직감에 의존하기 방식이기 때문에, 개개인의 편차가 크고 매우 비효율적인 방법입니다. 하지만 단순하고 탐색시간이 자유롭다는 장점이 있습니다.

2) Grid search

Grid search는 모든 hyperparameter의 경우의 수에 대해서 최적의 조합을 찾는 것을 의미합니다. 주어진 search space에서 쉽게 좋은 결과를 얻을 수 있다는 장점이 있지만, search space가 늘어날수록 기하급수적으로 탐색시간이 늘어나는 단점이 있습니다.

3) Random search

Random search는 각 hyperparameter의 최소, 최대값을 정해두고 범위 내에서 무작위 값을 정해진 횟수만큼 반복적으로 추출하여 최적의 조합을 찾는 것을 의미합니다. Grid search와 유사한 점이 있지만, random하게 일부 범위만 관측한 후 가장 좋은 값을 고르기 때문에 Grid search 보다 시간 대비 성능이 좋다고 알려져 있습니다.

실제로 Bengio 연구팀은 2012년에 발표한 논문에서 high dimensional hyperparameter optimization에서는 Grid search 보다 random search를 사용했을 때 성능이 더 좋을 수 있다고 밝혔는데요 [2]. 기타 연구들에서도 앞서 소개한 3가지 기법들 중 random search가 가장 좋은 결과를 도출한다고 주장한 경우가 많았습니다.

4) Bayesian optimization

Bayesian optimization은 단순히 무작위 추출을 반복하는 것보다, 기존에 추출되어 평가된 결과를 바탕으로 앞으로 탐색할 범위를 더욱 좁혀 효율적이게 시행하는 아이디어에서 시작되었는데요. 이 아이디어를 Bayesian theory 및 Gaussian process(GP)를 통해 구현한 것이 베이지안 최적화 방법입니다. 이 방법은 불필요한 파라미터의 반복 탐색을 줄여 시간 대비 탁월한 성능을 보인다는 장점이 있습니다. 이같은 이유로 현재 hyperparameter 최적화의 주류 이론으로 자리잡고 있으며, 최근에는 베이지안 최적화의 속도 향상을 목적으로 한 연구가 주로 진행되고 있습니다.

Bayesian optimization은 알려지지 않은 목적 함수를 최대/최소로 하는 최적해를 찾는 기법으로, surrogate model과 acquisition function로 구성됩니다. surrogate model은 현재까지 조사된 입력값-함숫값 점들을 바탕으로 f(x)를 추정하는 확률모델로, 보통 Gaussian Process가 주로 사용됩니다.

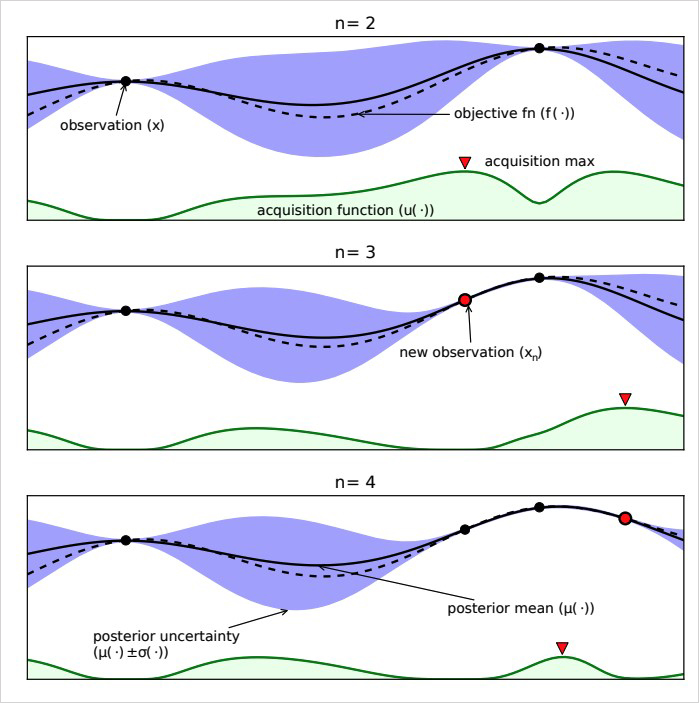
위 <그림1>은 3번의 반복 GP 연산 과정을 보여주고 있습니다. 먼저 검정색 점들은 현재까지 조사된 입력값-함숫값 점이고, 검정색 실선이 GP의 평균값 μ(x), 보라색 음영이 x 위치별 표준편차 σ(x), 검정색 점선이 실제 f(x)값입니다.

surrogate 모델을 통해 현재 확보된 데이터와 평가지표 간의 관계를 한눈에 확인할 수 있는데요. 예를 들어 σ(x) 값을 자세히 보면, 조사된 점(observation(x))의 값에서 멀어질수록 σ(x)의 값이 커지는 것을 확인할 수 있습니다. 이는 추정한 평균값 μ(x)의 불확실성이 커진다고 볼 수 있는데요.

아래에 존재하는 초록색 음영은 Acquisition function으로, 다음 입력 후보 x를 탐색하여 추천하는 역할을 합니다. Acquisition Function은 우리가 Black-box라고 가정하는 함수 f(x)에 대해 확률 추정 모델의 결과를 바탕으로, n+1 시점 입력값 후보 x를 추천하는 함수인데요. 여기서 acquisition function의 목표는 지금까지 나온 값들보다 더 큰 값이 나올 가능성이 제일 높은 점을 추천해주는 것입니다. 이때 최적 입력값 x는 조사된 점들 중 제일 높은 함수값 근처에 위치하거나, 표준편차가 최대인 점 근처에 위치할 가능성이 높습니다. 이 두가지 경우를 Exploitation, Exploration전략이라고 합니다.

Exploitation은 지금까지 주어진 정보에서 최고의 선택을 하는 것이고, Exploration은 더 많은 정보를 수집하는 것을 택하는 것입니다. 이때 새로운 정보를 수집하는 과정에서 표준편차가 최대인 점 근방에서 최적 입력값 x를 찾는 것을 시도하는데요. 이 두가지 전략이 적절한 균형을 잡을 수 있도록 하는 함수를 Expected Improvement(EI) 함수라고 합니다.

Bayesian Optimization in Trading

이번 파트에서는 주가 예측이 필요한 알고리즘 트레이딩에서 베이지안 최적화 기법을 어떻게 적용할 수 있을지, 제가 진행했던 간단한 실험을 바탕으로 설명드리겠습니다.

먼저 알고리즘 트레이딩은 기본적으로 투자자의 감정을 배제하고 사전에 설정한 원칙을 기반하여 매매하는 방법을 말합니다. 미리 설정된 매매 원칙을 이용하여 과거 데이터에 모의투자가 가능하다는 장점이 있는데요.

이때 사전에 계획된 트레이딩 전략이 효과적으로 잘 동작하는지, 과거 데이터를 통해 증명하는 것을 ‘백테스팅(Backtesting)’이라고 부릅니다. 쉽게 말해, 백테스팅은 과거로 돌아가서 테스트를 해보는 것인데요. 사실 과거를 완벽하게 재현한 것이 아니기 때문에 무조건적으로 신뢰할 수는 없습니다. 또한, 과거는 과거일 뿐, 과거의 성과가 미래의 성과를 보장하지는 않기 때문에 이러한 요소들을 감안하고 진행해야하는데요. 그럼에도 불구하고 백테스팅은 전략의 우위나 효과를 판별하기 좋은 도구입니다. 시기별 백테스팅을 통해 전략이 유효한 시기는 어떤 시기인지에 대해 힌트를 얻을 수 있습니다.

백테스팅을 하기 위해서는 데이터와 프레임워크가 중요한데요. 본 실험에서 데이터는 Finance DataReader, 백테스팅 프레임워크는 Backtrader을 선택했습니다.

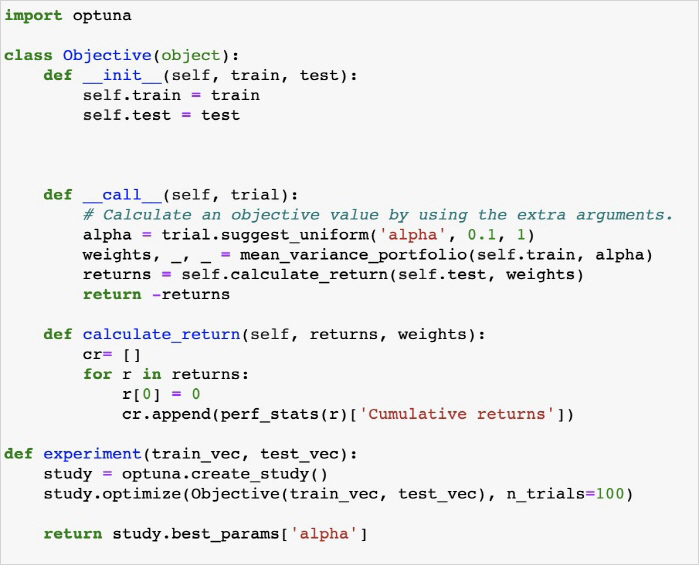
또한, Bayesian optimization을 트레이딩에 적용하기 위해서는 백테스팅 요소 외에도, 기본적으로 최적화해야 할 hyperparameter와 이를 사용하는 알고리즘이 필요한데요. optuna 프레임 워크를 통해서 Mean-Variance portfolio 알고리즘의 하이퍼파라미터를 최적화했습니다.

optuna를 선택하게 된 이유는 편리함과 확장 가능성 때문입니다. 아래 <표1>에서 각 프레임워크에서 제공하는 기능별로 비교하는 표를 보면, 해당 저자는 optuna가 가장 많은 기능을 제공하고 있다고 주장하는데요. 일반적으로 hyperparameter 최적화 기법에서 많이 사용되는 프레임워크인 hyperopt에 비해, optuna를 활용하면 algorithm trading에서 필요한 dashboard와 pruning을 사용할 수 있다는 장점이 있어 최종적으로 optuna를 선택했습니다.

mean variance model은 자세히 설명하기에는 너무 긴 내용이기 때문에 간단히 설명하자면 기대 수익에 대해 분산으로 표시되는 위험을 평가하는 모델입니다. 주어진 포트폴리오가 있을 때, 분산 대비 최대 수익율의 조합을 구하는 방법입니다. 시장은 상황에 따라 급변하는 특성을 가지고 있기 때문에, 최근 한달을 기준으로 목적함수를 최적화하여 최근 시장에 맞는 최적의 mean variance 식을 도출하고자 아래와 같은 식을 활용하였습니다.

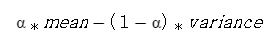
여기서 alpha라는 hyperparameter를 통해서 수익률을 목적으로 최적화할지, 변동성을 목적으로 최적화할지, 조절이 가능한 식을 만들었습니다. 다음 백테스팅에서는 포트폴리오 리밸런싱을 한 달마다 실행했는데요. 실행하기 전에 포트폴리오 리밸런싱 당일 기준으로 과거 한 달에 대해 alpha를 bayesian optimizer로 수익률을 최적화한 후, 다음 리밸런싱에 사용하였습니다.

이번 백테스팅에서 사용한 알고리즘은 코스피 30개 종목을 균등하게 매수하는 1/n porfolio, 위에 설명한 mean variance model과 bayesian optimization 기법으로 과거 1달의 수익률을 최적화한 mean variance model(bayesian mean variance model) 입니다. 이 3가지 알고리즘 모두 월 단위 기준으로 종목들의 비중을 조절하는 portfolio rebalancing을 진행했습니다.

또한, 여기서 백테스팅 환경은 아래와 같이 구성하였습니다.

KOSPI200
시가총액 30위
1/n portfolio, mean variance model, bayesian mean variance model
벤치마크 코스피지수
2015-01-01 ~ 2020_12-31
monthly rebalancing

Result

백테스팅은 그 자체로는 의미를 가지지 못합니다. 앞에서 언급했듯이 완전한 과거 환경을 구현하여 테스트를 진행할 수 없고, 과거의 성능이 미래에서도 무조건 잘된다는 보장이 없기 때문입니다.

이같은 이유로 필요한 것이 바로 성과분석입니다. 성과분석을 통해 전략이 어느 정도의 수익률을 달성했는지, Max Draw Down (MDD)는 어느정도였는지, 변동성이 심한 장에서 잘 견디는지 등에 대한 정보를 제공받을 수 있습니다.

아래의 <표2>는 pyfolio라는 성과분석 도구를 사용하여 분석한 결과이며, <표2>와 <그림3> 각각은 3가지 모델(1/n portfolio model, mean variance model, bayesian mean variance model)의 성과를 보여주고 있습니다. 여기서 bayesian mean variance model은 mean variance model과 bayesian optimization을 통해 hyperparameter를 최적화한 모델입니다.

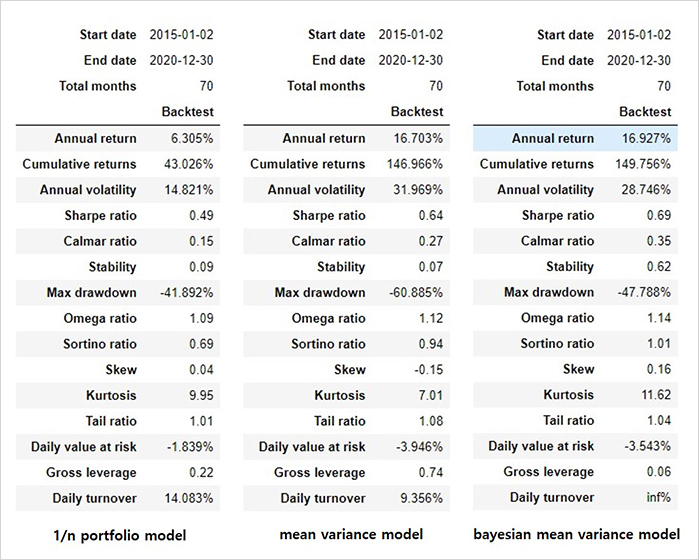
결과 비교는 2015년-01월-02일 부터 2020년-12월-30일 까지의 기간을 가지고, 앞서 이야기한 3가지 알고리즘 백테스팅 결과를 비교분석하는 방식으로 이루어졌습니다.

그 결과, bayesian mean variance model이 제일 높은 누적 수익률, 연평균 수익률을 기록한 것을 확인할 수 있었습니다. bayesian mean variance 모델이 주어진 기대수익률 하에서 리스크를 최소화하는 포트폴리오를 찾음으로써 전체 코스피 시장의 평균 수익률을 뛰어넘는 수익률을 보여주었습니다. 해당 모델이 mean variance model 보다 변동성이 적은 것으로 보아, hyperparameter 최적화를 통해 모델이 목표로 하는 리스크 최소화 측면에서 성능을 개선했다고 보여집니다.

또한, 1/n portfolio의 경우 동일한 비중으로 분산 투자한 결과, 연평균 변동성이 제일 적은 것으로 확인되었습니다. 각 알고리즘이 가지고 있는 hypothesis에 맞는 결과가 나왔다고 보여집니다. 다만, 기간 내 최대 수익률(300% 이상)의 경우 mean variance model이 높은 것으로 보아, 테스트 시점을 여러구간으로 나누어서 해보는 것도 좋은 방법으로 보입니다.

앞서 분석한 결과를 가지고 전략을 선택하게 된다면 최소의 연평균 변동성이 필요한 시기엔 1/n portfolio 전략을, 수익률을 극대화하고 싶다면 bayesian optimization이 적용된 mean variance model을 선택할 수 있을 것입니다. 이처럼 때에 따라 선택하는 전략이 다르듯, 백테스팅을 통해 시기에 맞는 인사이트를 얻어 알고리즘 트레이딩에 사용하는 것이 백테스팅의 역할입니다. bayesian optimization은 알고리즘 트레이딩에서 필수는 아니지만, 상황에 따라 최선의 선택이 될 수 있다고 생각하는데요. 오늘 소개드린 bayesian optimization과 알고리즘 트레이딩 내용이 도움이 되셨으면 좋겠습니다. 감사합니다.

참고문헌

[1] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, “Taking the Human Out of the Loop: A Review of Bayesian Optimization,” in Proceedings of the IEEE, vol. 104, no. 1, pp. 148-175, Jan. 2016, doi: 10.1109/JPROC.2015.2494218.
[2] Bergstra, James, and Yoshua Bengio. “Random search for hyper-parameter optimization.” Journal of machine learning research 13.2 (2012).
[3] Brochu et al., A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning.
[4] Bengio et al., Practical recommendations for gradient-based training of deep architectures.
[5] Akiba, Takuya & Sano, Shotaro & Yanase, Toshihiko & Ohta, Takeru & Koyama, Masanori. (2019). Optuna: A Next-generation Hyperparameter Optimization Framework. 2623-2631. 10.1145/3292500.3330701.
[6] https://en.wikipedia.org/wiki/AI_winter
[7] https://github.com/FinanceData/FinanceDataReader
[8] https://www.backtrader.com/
[9] https://blog.naver.com/dpfkdlt/221678800067
[10] https://blog.naver.com/steve5636/222279062968